01. 用語の定義
まずは,オンライン講義の様子をご覧ください(Youtube動画 約3分)

02. 面積・高さ・階数
まずは,オンライン講義の様子をご覧ください(Youtube動画 約2分30秒)
06. 一般構造

■学習のポイント
07. 既存不適格
「法86条の7」では,次の3つをチェックします.
問題文に「病院の用途を変更して,有料老人ホームとする場合」とあることから「類似用途だ!」と反応しがちですが,「確認申請が不要となる類似用途」と「既存不適格が継続となる類似用途」の似て非なる2つの類似用途があります.
08. 申請手続
さて,「建築主事と特定行政庁の違い」ですが,「建築主事」とは,行政側にいる建築の専門家だと理解して下さい.(全般に関して言えることですが,あくまで学科試験対策向けに建築知識を分かりやすく説明するための説明内容だと考えて下さい.)
法6条には,確認申請について規定されており,「申請義務が発生する建物(=確認申請書を提出しなければならない建物)」について定められています.ここで,「法6条各号」の区分については,暗記してしまいましょう(法規科目で数少ない暗記項目と割り切ってください).
「中間検査」(法7条の3)について補足説明しておきましょう.旧来は,確認済証の交付を受け,工事を着工し,工事が完了した後に,工事完了申請を提出し,完了検査を経て,検査済証を交付してもらう流れでしたが,この流れですと例えば,完了検査の時点で法令違反などの問題が発覚した場合,既に,完成してしまっている建物を壊して法基準を満たす形に作り変えることになります.また完了時には隠れて見えない部分についても,途中の段階で見ていれば修正可能だった不具合部分も,その時点で是正することが可能です.そこで,「特定工程」が定められます(「階数が3以上である共同住宅」という具体的な規模用途が記載された点に注意してください).建物の構造や規模にもよりますが,例えば,基礎の配筋完了時が「特定工程」として指定されている場合には,基礎の配筋という工事工程が完了した時点で,「中間検査の申請」を行い,「中間検査のチェック」を受けた後出なければ次の工事工程に進めません.つまり,工事を進めることができないということです.尚,中間検査の申請先も,確認申請や工事完了申請と同様に,建築主事でなく,指定確認検査機関にお願いしても構いません(法7条の4).
「仮使用」については,先述の通り,本来は完了検査済証を発行してもらわなければ,例え,建築主であろうと勝手に建物を使用することが出来ません(法7条の6).違反建築物として工事が完了してしまっている可能性もあるからです.建築主は,建築については素人でもあるので,自分が建ててもらった建物が違反建築物であるかどうかどうかの判断を適切に下すことができません.仮に,建築主自身が違反建築物であることを知った上でその建物を使用し,万が一事故が起きても自業自得ですが,そこに,建築主以外の第三者が違反建築物だと知らずに利用して,例えば,いきなりデパートや映画館の床が抜けて命を落とすことになったとしたら,社会的に大問題となってしまいます.ただし,法7条の6では,ただし書きで特例を設けてあります.その特例とは,例えば「特定行政庁が安全上,防火上,避難上の観点から考えて,完了検査済証が発行される前でも使用(=仮使用)してもよいと認めた場合」です.(平成27年の改正で「建築主事」と「指定確認検査機関」も所定の範囲で仮使用を認定することができるようになりました).
「仮使用」(法7条の6)と対比で覚えておきたいのが「安全上の措置等に関する計画の届出」(法90条の3)の話です.この規定は,一見,「仮使用申請」の話と似ていますが,全くの別モノだと考えて下さい.所定の建築物の場合,工事の施工中に建物を使用する場合には,仮使用申請とは別に,この「安全上の措置等に関する計画の届出」を特定行政庁に提出する必要があります.「仮使用申請」とごっちゃになって考えてしまう受験生も多いので,注意して下さい.以上を踏まえた上で,収録されている問題を解いて頂ければ,この項目の対策も万全でしょう.
「定期報告」(法12条)について,以前は,定期報告の実施要請を無視する建主や,精度の低い報告が少なからずいましたが,違法な増改築や,エレベーターによる死亡事故,遊戯施設による死亡事故などが起こり,運用の厳格化が行われました.また実際に健全な社会ストックの拡充という観点からも,注目される制度です(そういう観点からも出題は多い).建築物で言うと同条1項は「政令で定めるもの」と「特定行政庁が指定するもの」の2つあります.従来は,後者だけの規定だったのですが,現在は,全国共通で指定される用途・規模については「政令」で定めて,それから漏れたものを補完できるよう各地の行政庁が独自に指定する,という立て付けになっています.
最後に「用途変更」について簡単に説明します.法87条に,「建物の用途を変更して,変更後,法6条一号に該当する建築物となる場合には,用途変更による申請義務が生じる.」とあり,また,カッコ書きで,「類似用途(=映画館から劇場への用途変更というような同じ内容の用途への変更をいう)の場合は,用途変更による申請義務は発生しませんよ.」と規定されているわけです.類似用途(通称:類似特建)かどうかについては,令137条の18でチェックします.あとは,解説を読んで頂ければマスターできるはずです.要は,映画館として設計した建物の場合は,映画館という用途を踏まえて必要となる関係法令が適用され,それらの規定を全てクリアーした上で存在しているわけだから,類似用途である劇場に変更したところで,必要となる関係法令は,全てクリアーできているものとみなせるわけです.ただし,劇場からデパート(物品販売業を営む店舗等)への用途変更の場合は,劇場という用途について要求される関係法令と,デパートという用途に対して要求される関係法令は,全く異なる内容のものですので,その場合は,再度,確認申請を行って,デパートという用途に要求される関係法令を全て満たしているかどうかのチェックを受けなさい,という話ですね.
土地勘(とちかん)の無い街を地図を見ながら,標識を探しながら歩くのと,「喫茶店はココと少し先にもう1軒ある」「この角を曲がると近道だな」等,頭の中に街のマップイメージのある人の歩き方は,全く異なります.
法規科目を得意分野にするのは,この土地勘を習得することに似ています.
法令集のインデックスを頼りに「問題文と条文を照らし合わせて確認する」という解き方と,主要条文の構成や並びを理解して,法令をイメージしながら問題文を読む人の解き方は,全く異なります.
オンライン講義「法規」では「法令のイメージトレーニング」を用意しています.これは脳内の法令マップを作っていく助けとなります.【こちら】
大事なのは「法令集に細工する事」ではなく,「頭の中の条文構成で対処できるものを増やしていく事、実際に法令集を見た時に,構成や出題のポイントが浮き上がって見える事」その状況をどの範囲で試験までに準備できるかという事です.解説に頻出する条文だけで構いませんので,その意識で挑みましょう.
09. 構造
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
次に,「第8節」の「構造計算」です.「第1款・令81条」にある「構造計算方法の種類」について見てみましょう.
「令36条1項」では「耐久性等関係規定」という用語が定義されています.この「耐久性等関係規定」とは,「構造仕様規定」のうち,極めて重要な規定と解釈してください.「構造仕様規定」のうちの一部が,「耐久性等関係規定」です(包含関係).そして,難易度の高い(=精度の高い)構造計算により,計算した場合には,構造仕様規定を全て満たさずとも「耐久性等関係規定」だけを満たせばよい(=構造計算で安全性を担保している)ことになります(耐久性等関係規定「以外」の構造仕様規定は,適用除外).

次に「令82条」以降を解説します.令82条の条文名が「保有水平耐力計算」となっていますが,このことで多くの受験生の皆さんが混乱することとなります.令82条前段に「・・・保有水平耐力計算とは,次の各号及び次条から第八十二条の四までに定めるところによりする構造計算をいう」とあります.
10. 耐火構造等
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
■学習のポイント
「耐火性能・耐火構造・耐火建築物」など,似たような用語が多く,紛らわしく感じられるかもしれませんが,まずその3点を意識して,キチンと整理して,体系的に学習していってください.
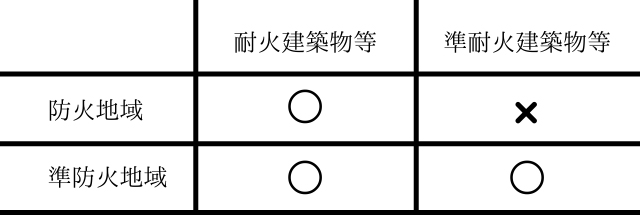
12. 防火地域
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
13. 防火区画
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分30秒)
次に,防火区画の種類について,区画の仕方(=ブロック分けの仕方)によって,次の4種類に分けられます.
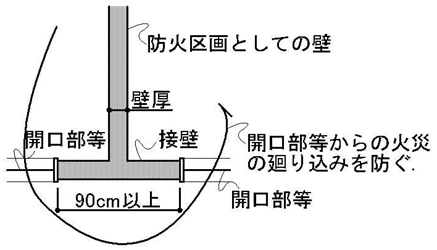
最後に,「16項」の「接壁」について補足説明しておきます.この接壁とは,次のようなイメージです.
14. 内装制限
まずは,オンライン講義の様子をご覧ください(Youtube動画 約6分)
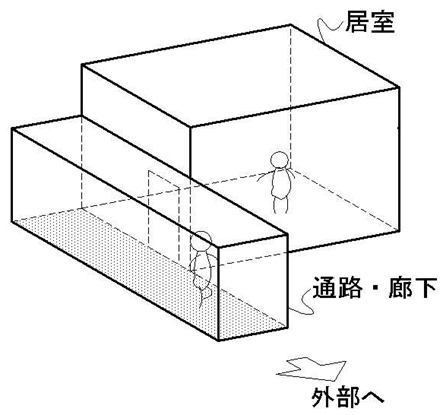

15. 避難施設
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
最後に, 「避難」に関連するその他の規定を学習します.例えば,「排煙設備」,「非常用照明」,「非常用進入口」の話となりますが,これらに共通するのは,まずは,「設置基準(設置義務が発生する条件)」を抑えること,その隣の条文には,設置する場合にどういった仕様(構造)で設置すればよいのかという条件が説明されているという流れとなっています.
17. 建築制限
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分)
18. 容積率・建蔽率
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分)
次に「建蔽率」です.「建蔽率」には,法定建蔽率しか存在しません.そのため,「法定建蔽率=最大建蔽率」となります.図問題の場合,法定建蔽率は,問題文に記載がありますが,「商業地域」は「8/10」しかありませんので,数値の記載はありません.
■学習のポイント
イレギュラーなパターンとして「問題コード20151」は,用途を「共同住宅」と前提として,「共用通路緩和」や,「駐車場1/5緩和」を取り入れる問題となっていますが,その知識は過去問レベルの内容ですので,最後の床面積の増減の考え方だけ間違わなければ,対応も可能です.
法規科目は時間が足りず「図問題は後回し」にする受験生は多いです.自分にとって難しい問題を後回しにするのは戦略としては王道ですが,図問題でも「その場でトライすべき問題」と「後回しにすべき問題」があるはずです.過去問の知識の範囲で構いませんので,本試験までに,各自で仕上げるレベルを想定しておきましょう.
19. 高さ制限
まずは,オンライン講義の様子をご覧ください(Youtube動画 約3分)
「法56条」の構成を確認しましょう
続いて隣地斜線です.隣地斜線の緩和措置は,次の3種類となります.
最後に,北側斜線です.北側斜線は,敷地が1・2種低層住専(+田園住居)又は1・2中高層にある場合のみ適用される高さ制限です.「1・2種低層住専」は,図問題での出題は考えにくいので,実質,「1・2中高層」かどうかをチェックします.それ以外なら「北側斜線の検討不要」となり,計算するボリューム(時間)が大きく異なりますので,これを1番先にチェックします.
20. 地区計画
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分30秒)
「地区計画」には,「市町村が定められる条例による制限」があります.皆さんが実際に,建物を設計する場合には,建築基準法だけを守ればよいというわけではありません.各自治体ごとに「条例」というものが存在するためです.例えば,東京都の場合には,「東京都安全条例」という東京都版の建築基準法のようなものが存在しますし(ちなみに,法令集程度の厚さがあり,書店で購入することが出来ます),横浜市の場合には,横浜市条例というものがあります.よくある失敗談として,基準法上は適合しているが,条例に違反している設計をしてしまったという話を聞きます.基準法同様の扱いとして確認申請の際にチェックを受けます(基準法6条の「建築基準関係規定」)ので確認申請が下りません.勿論,条例の中には,基準法に掲載されていない規定も出てきます.東京都安全条例で言えば,「窓先空地」,横浜市条例でいえば,「2方向避難」などです.
建築基準法では「法68条の2」に,「市町村は,地区整備計画等が定められている地区計画等の区域においては,建築物の構造等の制限を条例として定めることができる.」とあります.この「地区整備計画等が定められている地区計画等の区域」とは,分かりやすく言えば「街づくりのルールが具体的に決まっている地域」といったイメージです.そういう地域においては,「条例で制限をかけてもいいですよ」という意味になります.上記のように「条例として制限をかけ場合」は,基準法同様の扱いとなります.次に,その2項に,「前項の規定は,政令で定める基準に従って行うこと.」とあります.この「政令で定める基準(通称:政令基準)」という言い回しには,慣れましたでしょうか.これは,「施行令の方に定めている具体的な内容」という意味です.この政令基準は,「令136条の2の5各号」とあります.例えば,その「二号」に「建築物の容積率の最高限度は,5/10以上の数値としなさい.」とありますが,これは,市町村は地区計画上の条例制限として,「容積率の最高限度」を定めることができますが,その場合には,「5/10以上(50パーセント以上)にしてあげなさい.」という意味です.通常,容積率は,100パーセントだとか,300パーセントといったものですが,建物のボリュームをあまり大きくしたくない場合には,地区計画上の条例制限として,容積率の最大限度を決めることができます.
尚,地区計画について,ある程度体系的に把握しておきたいという場合は,東京都のサイトの解説を参照ください.【こちら】
また,ネットで「○○市 地区計画」として検索してみてください.どんなことが定められているのか,をご自身の知っている街並みで確認することで,よりリアリティのある規定として定着します.
22. バリアフリー法
まずは,オンライン講義の様子をご覧ください(Youtube動画 約3分)
バリアフリー法(高齢者,障害者等の移動等の円滑化の促進に関する法律)の概略をおさえてしまいましょう.最初に用語の確認です.
□「特定建築物」 とは?
法2条十六号に定義されており,分かり易く説明すると,「学校,病院,事務所や共同住宅のように,利用者数の多い建築物」のことです.
□ 「特別特定建築物」 とは?
法2条十七号に定義されており,分かり易く説明すると,「特定建築物のうち,不特定多数の人が利用する百貨店などの特定建築物や,高齢者が利用する老人ホームなどの特定建築物」のことです. 尚,ここで注意して頂きたいのは,「特別特定建築物」は,「特定建築物」の一部であることです.これは,これまで勉強してきた「耐火建築物」と「準耐火建築物」の関係と一緒です.つまり,「特別特定建築物」は「特定建築物」に含まれている(包含関係)という事は理解しておきましょう.
「銀行は,特定建築物ですか?」といった具合に問われた場合は,このバリアフリー法2条十六号,十七号から「政令」をチェックします.例えば,法2条十六号に,「特定建築物とは,学校などの多数の者が利用する政令で定める建築物をいう.」とあります.建築基準法でも同じような言い回しが頻繁にありましたね.「政令」とは,「施行令」のことです.建築基準法の場合は,建築基準法の施行令というものがあり,同様に,バリアフリー法の場合も「施行令」というものがあります.したがって,「政令で定める」という言い回しがある場合には,「施行令の方で具体的に定めています」という風に頭の中で読み替えるようにして下さい.これだけで,条文をよりスムーズに読解できるようになります.では,具体的にどのような建築物が「特定建築物」とみなされるのかについて施行令4条を見てみましょう.そこに,バリアフリー法上,「特定建築物」としてみなされる建築物の一覧があります.ここをチェックすれば,問題文にある「銀行は,特定建築物ですか?」という問いに解答することができるわけです.「特別特定建築物」の場合も同じような要領で施行令5条を見ます.
次に,「建築物特定施設」という用語を覚えましょう.「建築物特定施設」とは,法2条十八号に規定されており,「出入口などで,施行令の方で具体的定められているものを建築物特定施設という.」とわかります.施行令6条に,具体的に定められている出入口や,廊下,階段などです.例えば,問題文で「昇降機は,建築物特定施設に含まれますか?」と問われたら,この施行令6条をチェックすれば一発で判断できます.非常に簡単ですね.
さて,次に,バリアフリー法の「基準」について説明しておきましょう.ここでは暗記することよりも,流れをマスターしてください.建築主等は,「特定建築物」を建築しようとする場合,「建築物移動等円滑化基準」というルールに適合するよう「努力」しなければなりません(法16条).また,「特別特定建築物」を建築しようとする場合,ある一定の規模については,「建築物移動等円滑化基準」というルールに適合させる「義務」があります(法14条).建築物移動等円滑化基準については,建築物特定施設である「出入口」の幅は,これくらい取りなさいとか,「駐車場」は,こういう具合に計画しなさいなどといった具体的なルールです.ここでの基準は,最低限の基準であって,より本格的に建築物をバリアフリー化するのであれば,更にワンランク上のルールがあります.それが,「建築物移動等円滑化誘導基準」と呼ばれるものです.「建築物移動等円滑化基準」よりも厳しく設定されております.これはどういったときに適用されるかというと「計画の認定」を受ける場合です(法17条3項第一号),
では,「計画の認定」とは何でしょうか.これは,「特定建築物(特別特定建築物を含む)を建築しようとする建築主等が,所管行政庁に,その計画内容について認定してもらうことができる.」というものです(法17条).義務ではなく自ら申請し,厳しい基準クリアし,認定を受けた特定建築物を「認定特定建築物」と言い,「容積率の特例」(法19条)や認定を受けたことを世間にアピールできる「表示」(法20条)等のメリットがあります.
上記の話を踏まえた上で,まずは,問題を解き進めていきましょう.収録問題を解き進めていくうちに,徐々に,知識をコントロールしている感覚が沸いてくると思います.この感覚こそ,学科試験に合格する際の感覚だと思ってください.この感覚を法規科目全般に渡り,また,全教科に渡り,広げていってください.ただし,肝心なのは,細かい部分にとらわれれ過ぎずに,法令集の構成を意識しつつ,その流れをマスターすることです.
■学習のポイント
この項目では,用語の意味や手続きの手順を確認するための問題がよく出題されますが,その分,「ケアレスミス」が起きる可能性も高くなってきます.「努力義務」と「義務」の違いや,「円滑化基準」と「円滑化誘導基準」の違いなど,普段なら取り違えないような事も読み落としたり,勘違いが発生したりするものです.無駄な失点は「読み落とさないぞ!」とか「条文と一言一句,照らし合わせてやる」という手法では防げません.上記のように体系的なイメージの中で問題文がどの辺りの話を聞いているのか,まずはその意味合いで問題文を捉えることです.その習慣や意識こそが本試験でのケアレスミスの防止に繋がります.
23. 耐震改修法
まずは,オンライン講義の様子をご覧ください(Youtube動画 約6分)
■学習のポイント
24. 建築士法
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分30秒)
■1級建築士の業務範囲(士法3条)
つまり,木造の場合には,階数が2以下,かつ,高さ13m,軒高9m以下で,延べ面積が100㎡以下であれば,無資格でも設計・工事監理する事ができます.「建築士の業務範囲」は,JAEICのホームページにも掲載されているので,一度,条文と照らし合わせておくと良いでしょう.【こちら】
ここで,頻出されるポイントについて,いくつかお話しておきましょう.
新問に対して「その根拠条文を法令集から探し出す」という手順に固執している場合,線引きをしていない部分は相当読み辛く,試験中に実践するのは困難です.一方で,気になった箇所を闇雲に線引きしたりインデックスを貼りまくってしまうと,余計みにくい法令集となってしまいます.重要なのは,問題文や法体系の勘所を養うことです.これは「ヤマ勘に頼る」ということではありません.例えば「定期講習」に関する出題があったとき,まずは建築士法の「目次」をみてみましょう.まずは,「どの章に属する内容なのか」を推測します(「建築士法の”章”」については,一通り読んでみてください).定期講習は6章の「建築士事務所」よりも建築士個人の話だし,法改正の概要を知っていれば,2章の「免許」や3章の「試験」ではなく「業務」に近い話だとわかります.内容は全く新しいものですので追加されていること推測してみると,「業務」の章の最後の方に記載されていることがわかります(士法22条の2).こういった具合に,法の構成から推測する手法を覚えておいてください.また,ある選択肢の内容が「対」になっていたり,他の選択枝と明らかに毛色が違っていたりする場合がありますので,注意深く,問題文中にある「手がかり」を読み取ってください.
26. 都市計画法
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分30秒)
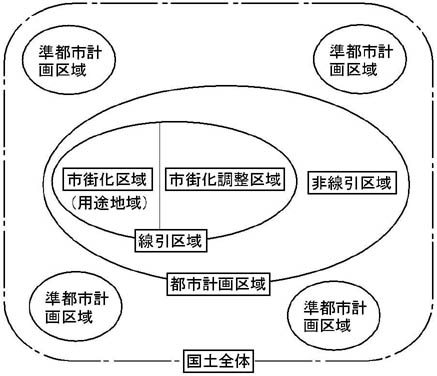
それでは ,都市計画法上の用語を学習しましょう.都計法4条をご覧ください.必ず法令集を開き,条文で全体構成を把握するように心掛けてください.
開発許可の条文の構成をみてみましょう.ポイントは「主体は誰か」です.これはそのまま「手続きの流れ」を表しています.各条文の1項だけでよいですから,通して確認してみてください.
02.現場管理
まずは,オンライン講義の様子をご覧ください(Youtube動画 約2分30秒)
まずは,過去問題の解説部分を流し読みして下さい.
この項目では,安全衛生管理体制や作業主任者の選任などの建設工事現場の安全に関する出題となっています.なお,請負契約に関しては,「請負契約」のインプットのコツでまとめて説明します.また,材料の保管・管理方法などに関しては,各工事項目に収録されております.それぞれの項目のインプットのコツを参考にしてください.
安全衛生管理の部分は似たような言葉が多く,イメージしにくい内容です.
大まかな安全衛生管理体制と,そこに出てくる言葉の意味を理解しましょう.
工事現場の安全確保のため,現場代理人(現場所長)が責任者となり,建築基準法や労働安全衛生法,その他関係法令などに従い工事現場の安全衛生に関して管理を行っていきます.
ここで,総括安全衛生管理者という言葉が出てきます.これは,労働安全衛生法第10条,労働安全衛生法施行令第2条により,業種ごとに一定規模以上の事業場に選任が義務づけられているものであり,その基本的な考えは,労働災害を防止する責任は,本来事業者にあると考えられますので,その事業を統括管理する者を総括安全衛生管理者として選任させて,安全管理者または衛生管理者を指揮させ労働者の健康と安全を確保する業務を責任を持って統括してもらう人という風に定義されています.ここで,安全管理者及び衛生管理者とは,総括安全衛生管理者の業務のうち,安全・衛生に関わる技術的事項を管理する人を指します.この総括安全衛生管理者は,常時100人以上の労働者を使用する事業場ごとに選任する必要があります(問題コード24023).
似たような言葉として,統括安全衛生責任者という言葉があります.これは,労働安全衛生法第15条,労働安全衛生法施行令第7条により仕事の一部を請負人に請け負わせている者のうち建設業,造船業について一定規模以上(労働者数)の仕事(現場)ごとに選任が義務づけられているものであり,その基本的な考えは,建設業および造船業の事業場においては,元方事業者および下請事業者の労働者が同一場所で混在して作業を行っている為,他業種に比し災害発生率が高率となっているのでこの混在作業から発生する労働災害を防止するため,元方事業者(特定元方事業者)に統括安全衛生責任者を選任させて,各事業者間の調整をおこなってもらうことにより工事現場等で働く労働者の健康と安全を確保してもらうという風に定義されています.この統括安全衛生責任者は,特定元方事業者(元請負者)と請負人とが混在し,常時50人以上の労働者を使用する事業場ごとに選任する必要があります.
総括安全衛生管理者,統括安全衛生責任者ともに,事業所(現場)の規模(100人以上 or 50人以上の混在現場)に違いはありますが,通常,現場所長などがこれに当たります.
事業者は,労働災害を防止するための管理を必要とする作業においては,免許を受けた者または技能講習を終了した者のうちから作業主任者を選任し,その作業に関わる労働者の指揮などを行わせなければなりません.
では,作業主任者を必要とする作業と必要としない作業についてまとめてみましょう.
作業主任者が有資格者でなければならない作業としては,ガス溶接作業主任者があります.
作業主任者が技能講習終了者でなければならない作業としては,
地山の掘削作業主任者(問題コード28022)
石綿作業主任者(問題コード01022ほか)
コンクリート造の工作物の解体等作業主任者(問題コード01021)
型枠支保工の組立等作業主任者(問題コード13033)
足場の組立等作業主任者(問題コード01024ほか)
建築物等の鉄骨の組立等作業主任者(問題コード17033)
土止め支保工作業主任者(問題コード01023ほか)
などがあります.
それぞれの作業内容については,上記問題コードを参考に,解説を読んで理解しておいて下さい.
■学習のポイント
ISO9000シリーズ(品質関係)やISO14000シリーズ(環境問題関係)などに関しては,過去問の解説程度の基本的な理解で十分であると思います.
この項目も,過去問20年分の「知識」の理解で十分対応可能な項目であると思われます.






