03.伝熱
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
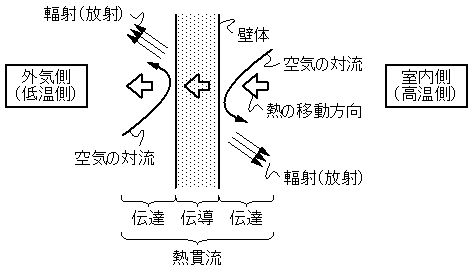
この項目の学習を効率よく進めるために,「熱」に関する基本事項を学ぶことから始めましょう.解説集として収録されている「熱の解説」をまず最初にご覧ください.次に,問題解説をザッと読み進めます.この時,文章を映像化して読むことを意識しましょう.例えば,冬期をイメージして下さい.冬期には,室内側が外気側に比べて高温となるため,熱は,室内側から外気側へと流れることになります(熱は,高い方から低い方へと移動する).その際,建物の外壁を通過するわけです.このときの熱の流れを考えてみましょう.まず,室内側の空気から外壁の室内側表面へと熱が伝わります.このように,空気から壁体へと熱が伝わることを「伝達」といいます.次に熱は,壁体内部を外気側へと伝わっていきます.このように,壁体中を通過する熱移動を「伝導」といいます.最後に,外壁の外気側表面より,外気へと熱は伝わります.このとき,壁体から空気へと熱が伝わるので「伝達」となります.このような「伝達」→「伝導」→「伝達」という熱の流れを総称して熱貫流と呼びます.
熱とは,物体を構成する分子の振動だと考えて下さい.中学校や高校時代に習った分子のモデル図をイメージしてみましょう.あの物体を構成している(例えば,アナタ自身も分子で構成されています)分子の振動こそ「熱」エネルギーの正体です.物体同士が隣り合うときに,その境界線が出来ますが,境界線に高温側の分子がドンドンとぶつかることによって,熱(=分子の振動エネルギー)を低温側の物体の分子へと伝えていくわけです.そのため分子の数が多ければ多いほど,物体間の境界線にぶつかる分子の数も増えますので,熱は伝わり易くなります.
また,伝熱計算に関する問題は,「伝熱」という仕組みを理解するために非常に重要な項目ですので,是非この機会にマスターしておきましょう.発展的な思考の源となります.まずは,下記解説をお読みください.
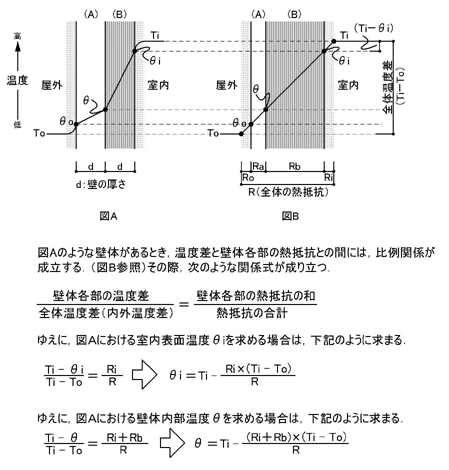
一見,難しい内容に見えますが,図Aの横軸は「壁の厚み」,図Bの横軸は「熱抵抗」です.図Bのように熱抵抗を横軸,壁体内部の温度差を縦軸として考えた場合,このように比例関係が成立します(熱抵抗の割合を表現).ちなみに,比例関係となる場合,一定の割合での増加・減少を意味し,グラフにした場合,直線で示すことができます.図Bの部材がコンクリートと断熱材なら,部材(B)の熱抵抗が大きいことから,こちらが断熱材に相当する部分と考えられます.
壁の熱貫流抵抗(㎡・K/W)を求める式 Rt=ri+Σrk+ro があります.
ri=内表面熱伝達抵抗
rk=熱伝導抵抗
ro=外表面熱伝達抵抗
ここで重要なのは「熱抵抗値」で単位が統一されている点です.
これらの熱伝導に関する熱抵抗値を「熱伝導比抵抗」といい,これに壁体を構成する各部材の厚み(d)を掛けたものの総和が「熱伝導抵抗(=壁体全体の熱抵抗値)」となり,それに壁の外・内で接する空気の伝達による熱抵抗値を加えることで,全体の熱抵抗値である「熱貫流抵抗」が求まります.この「熱貫流抵抗」の逆数が「熱貫流率」となります.
■学習のポイント
コード28042,23042,02022,21102,18023,02023ように,「熱貫流の仕組み」について,キチンと理解するのは当然として,「仕掛け方」にも注意していきましょう.出題も毎回同じ言い回しとは限りません.解説が多少長い問題コードは,それだけ丁寧な理解が必要となります.平成27年に図問題として出題された問題コード27031は,まさに総合的な理解が問われました.この項目の最重要問題と位置づけて,キチンと理解しておきましょう.
熱貫流抵抗[㎡・K/W] ←逆数→ 熱貫流率[W/㎡・K]
↑
(全体の熱抵抗値の総和)
↑
外側熱伝達抵抗[㎡・K/W] ←逆数→ 外側熱伝達率[W/㎡・K]
内側熱伝達抵抗[㎡・K/W] ←逆数→ 内側熱伝達率[W/㎡・K]
熱伝導抵抗[㎡・K/W] ←逆数→ 熱伝導係数[W/㎡・K]
↑
(各構成部材の熱伝導比抵抗に厚み[m]を掛けた総和)
↑
熱伝導 比 抵抗[m・K/W] ←逆数→ 熱伝導率[W/m・K]
これらは丸暗記するよりも,単位とその意味に着目しながら,仕組みを理解しておくことが大切です.






