06.トラス
学科試験における「トラス」の問題は,以下の仮定に基づいています.
・全ての部材が直線で,三角構成された骨組み
・節点が全てピン接合
・外力(集中荷重のみ)は節点にのみ作用
ポイント1.「節点には曲げモーメントは生じない.各部材に生じる応力は軸力のみ!」
上記,仮定に基づいているため,ポイント1.が言えます.それによって,問題を解くという行為が容易になるわけです.
次に,問題を解くという行為をより容易にするために
ポイント2.「ゼロ部材を探せ!」
「ゼロ部材」とは,応力(軸力)が生じない部材のことです.「トラス」の問題は,ある外力がかかる構造物において,ある部材に生じる応力はいくつになるでしょう?という問題ですから,「ゼロ部材」を探しだし,その部材を無視して考えると,より容易になります.
具体的には,節点に2つの部材が接合されていて,その節点に外力(反力)が作用していない場合には,その2つの部材に生じる応力はゼロである.ということが言えます.
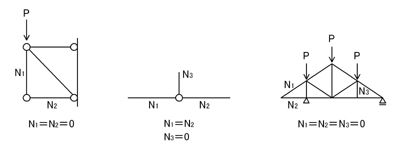
建築士の学科試験のトラス構造物の問題は,「力は釣り合っている」わけです.「外力(反力)」も,それによって生じる「内力(軸力)」も釣り合っているわけです.例えば,上記図の真ん中の図において,N3がゼロでなければ,N3の内力に釣り合う力が存在しません.N1に関しては,「大きさが同じ」で「向きが逆」であるN2と釣り合うことで,「力の釣り合い」は成立できます.つまり,N3=0と考えることができます.
実際に問題を解く際に,「ゼロ部材」を鉛筆などで塗りつぶしてみると,部材数が減って,問題が簡単になります.
ポイント3.「切断法」「節点法(示力図は閉じる)」をマスターしよう!
トラス構造物では,上記の仮定に書いてあるように,「軸力しか生じなく」かつ「内力も釣り合っている」ため,問題解法として「節点法(示力図は閉じる)」という方法が使えます.これは,06-1「トラス」の解説内の『部材に生じる軸力を求める場合,節点ごとに考えていく』に説明してあります.また「切断法」に関しては,06-1「トラス」の解説内の『Nfgを違う解法で求める』に説明してあります.
ここで,
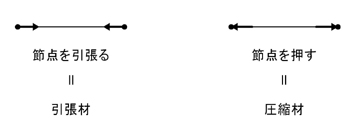
引張材と圧縮材は,上記図のようにルール付けします.逆に考える人も多くいるので注意して下さい.
「トラス」の問題の基本的な解き方としては(静定構造物であるので),「外力系の力の釣り合いを考える」→「内力系の力の釣り合いを考える」という2つの計算しかありません.
「外力系の力の釣り合い」とは,「外力(集中荷重)」によって,「支点反力」生じます.それを求めることを指します.
「内力系の力の釣り合い」とは,「外力(集中荷重)」によって生じた「内力(軸力)」を求めます.「節点法(示力図は閉じる)」や「切断法」によって求めることを指します.
「切断法」のポイントとしては,
・「切断する部材」は3つ以下
・具体的な計算としては,ΣM=0,あるいはΣY=0のどちらか
となります.
03051と21051について補足説明させていただきます.
通常のトラスの問題は「部材○○に生じる軸方向力はいくつか」という問題文であるのに対し,この問題は「ローラー支点の水平方向(横方向)の変位δBはいくつか」という問題ですね.
この問題を見たときに「通常のトラスの問題とは違うぞ.どうしよう??」と思った後で,「んん?求めたいのは水平変位δで,『それぞれの部材は等質等断面とし,断面積をA,ヤング率をEとする』の部分って,どこかで見たことがあるぞ!」という風に考えられるかがポイントです.
『ひずみ度ε(イプシロン)とは,長さLの部材が外力PによってΔLだけ変形した際に,ε=ΔL/Lと定義するものです.
ヤング係数Eとは,外力がかかった際の部材の変形のしにくさを表す指標であり,ヤング係数(E)=垂直応力度(σ)/ひずみ度(ε)で表現することができます.式を変形すると,垂直応力度(σ)=ヤング係数(E)×ひずみ度(ε)と表すこともできます.
部材にかかる外力(軸方向力)をN,部材断面積をAとすると,外力Nにより部材に生じる内力(σ)はσ=N/Aと表すことができるので,N/A=E×ΔL/L,これより,ΔL=NL/EAとなります.
このように「現象を数式化し,関係式を導き出す」ことが,構造(力学計算編)を得点源にする最大の要因の一つであることを理解してください.』
の部分が思い出されるかが解ける,解けないの分岐点になることがわかると思います.
「節点法」のポイントに関しては,「節点法」のインプットのコツを参照して下さい.
■ 学習のポイント
この「トラス」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.
しかし,上記「トラス」の3つの重要ポイントを駆使しても考え方がわからない問題は,一番後回しにすることを薦めます.






