06-1.節点法の解き方
トラス構造物の問題を解く方法に,切断法と節点法の2種類があります.更に節点法の中には,数値計算法と図式法の2種類があります.
その節点法の中の図式法のことを「示力図は閉じるで解く方法」と呼ぶこともあります.
今回は,この図式法について説明します.
まず,前提条件として,トラス構造物の問題は静定構造物であることがあります.ということは,力は釣り合っているわけです.
外力系の力の釣り合いで考えるとトラス構造物全体に関して,力は釣り合っていることがわかります.
内力系の力の釣り合いで考えると,トラス構造物全体が釣り合っているためには,各節点も釣り合っていることになります.
そこで,各節点ごとに,内力系の力の釣り合いを考え,力は釣り合っていることを数値計算ではなく図解法として行う方法に図式法は位置します.
それでは具体例で説明していきましょう.
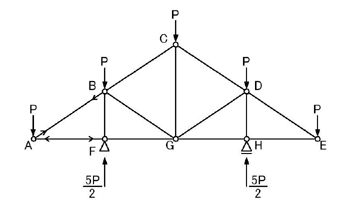
下図の問題で説明していきます.
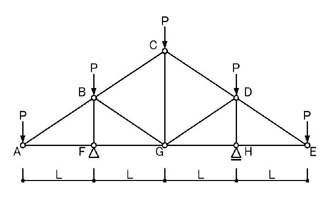
のような問題です.
静定構造物であるため,外力系の力の釣り合いを考え,支点反力を求めます.
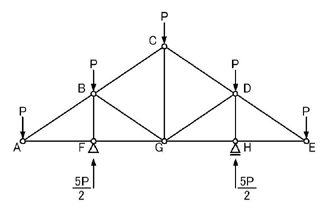
のようになります.
次に,ゼロ部材を探します.ゼロ部材に関しては「トラス」のインプットのコツのポイント2.を参照してください.
この問題の場合は,セロ部材はありませんね.
ポイント1.図式法では,未知力が2つ以下の節点について,力の釣り合いを考える!
このポイントは覚えてください.
なぜなのでしょうか.
簡単に言うと,未知力が3つ以上の節点について力の釣り合いを考えてみても,解くことができないからです.
上図において,左右対称であるため,左半分について考えます.
A点,B点,C点,F点,G点のうち,未知力が2つ以下の場所を考えます.
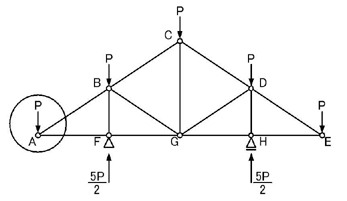
A点の未知数が2つですので,A点について考えてみましょう.
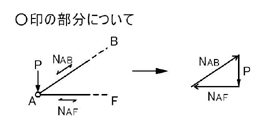
「節点で力が釣り合っている」=「示力図は閉じる」わけなので,節点Aに加わる力(外力P,NAB,NAF)の始点と終点とを結ばれる一筆書きができるように力の足し算を行います.上図の右図ですね.
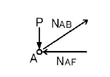
つまりA点での力の釣り合いは上図のようになります.
NABは節点を引張る方向の力であるため引張力で,NAFは節点を押す方向の力であるため圧縮力であることがわかります.
それを,問題の図に記入してみます.
のようになります.AB材は引張材であることがわかり,B点に関してNBAは節点を引張る方向に生じていることがわかります.同様に,AF材は圧縮材であるとわかり,F点に関してNFAは節点を押す方向に生じていることがわかります.
続いてB点,C点,F点,G点において,未知力が2つ以下の部分を探します.
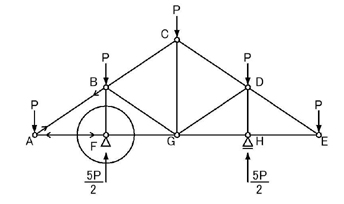
F点が該当しますね.
F点について力の釣り合いを考えて見ます.
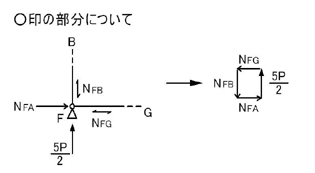
上図の左図にあるような各力が閉じるようになるためには,上図の右図のような力の向きであればよいことがわかります.
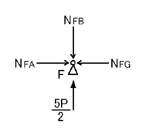
以上により,F点に関しては,上図のような力の釣り合いが成り立つことがわかります.
これを問題の図に記入しましょう.
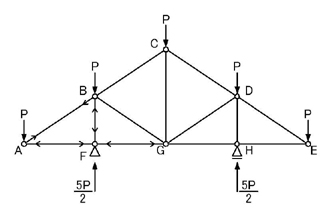
のようになります.
次にどの点について考えればよいでしょうか.
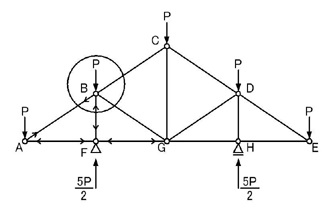
B点ですね.
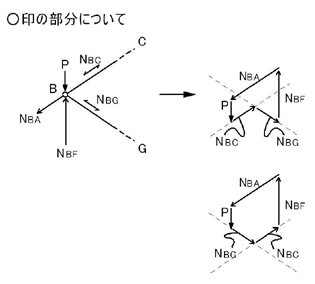
上図の左図のような各力が閉じるようにするためには,どうすればよいでしょうか.
上図の右図の上図でも下図でも閉じていることがわかります.
好きな方でいいので,各力が閉じるときの,各力の方向を自分で求められるようになってください.
以上の図より,NBCはB点を引張る方向の力,NBGもB点を引張る方向の力であることがわかります.
これを,問題の図に記入します.
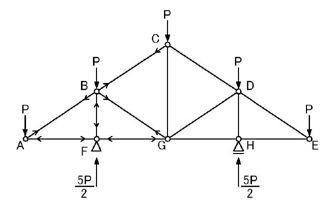
のようになりますね.
この問題は架構も外力も左右対称であるため,各部材に生じる応力も左右対称になることはイメージできるでしょうか.
そうすると,
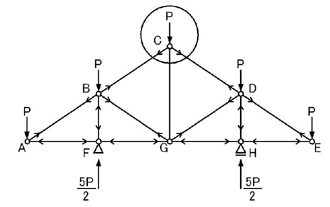
のようになります.
続いて,C点に関して力の釣り合いを考えて見ましょう.
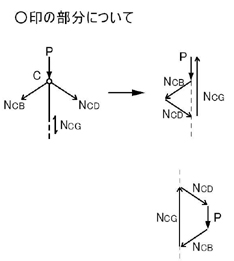
上図の左図にあるような各力が閉じるようになるためには,上図の右図のような力の向きであればよいことがわかります.右図の上図でも下図でも閉じていればいいのですから,どっちでも構いません.
どちらの示力図でもNCGはC点を押す力(圧縮力)であることがわかります.
これを問題の図に記入すると
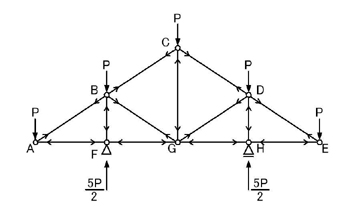
のようになります.
以上のことにより,「節点法」で各部材に生じる軸力が引張力か圧縮力であるかが判別することができます.
この問題のように,引張材か圧縮材かという問題に関しては,節点法の図式法で求めることができます.
しかし,ある部材に生じる軸力の値を求める問題に関しては,各節点での力の釣り合いを考えるときに,各力の値も求めなければなりません.
その際,「三四五の定理」や「ピタゴラスの定理」などの知識が必要になってきます.その辺は,00基礎知識の解説を参照してください.
また,図式法で各節点での力の釣り合いを考えるときに,例えば上記問題のC点におけるNCGと外力Pのように,向きが逆の力が出てくる場合に,各力の大きさの大小関係がわからないと,図式法で上手く示力図を描けない場合があります.
その時は,例えば上記問題のように全ての部材の長さがわからない場合,あるいは,角度が分からない場合には,各自で適当に決めてしまう方法があります.
例えば,
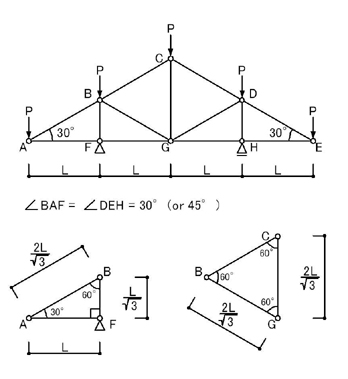
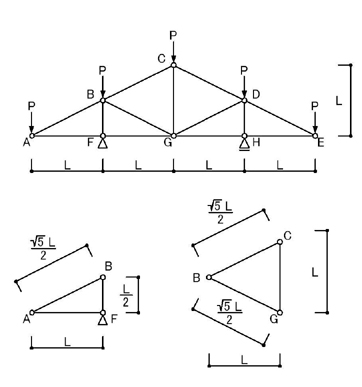
のように,∠BAF=30°であるとか,CG材の長さをLとかにして,「三四五の定理」や「ピタゴラスの定理」の定理を使いながら図式法で求めていく方法です.
この節点法に関しては,非常に多くの質問が来ます.また,各節点に関する示力図をまとめた「クレモナ図」についても質問が来ます.
ですので,「節点法を機械式に解く方法」という資料を作成しましたので,目を通しておいて下さい.【こちら】
■学習のポイント
トラス構造物として,図式法にとらわれ過ぎないように注意して下さい.問題によっては,切断法の方が簡単に求めることができます.切断法,図式法ともに解法を理解した上で,自分で使い分けられるようになってください.使い分けられるようになるためには,過去問で練習する方法が非常に有効です.






