07-2.モールの定理(その2)
単純梁や片持ち梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法に関しては,「モールの定理(その1)」のインプットのコツを参照して下さい.
今回は,単純梁,片持ち梁以外の架構にモールの定理を使う場合について考えて見ます.
まずは,連続梁の解き方について考えて見ましょう.連続梁とは,下図のように,ピン接合点や連続梁の支点を持つ架構を指します.
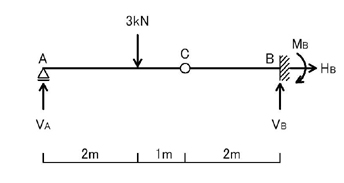
ここで,支点についてまとめてみましょう.
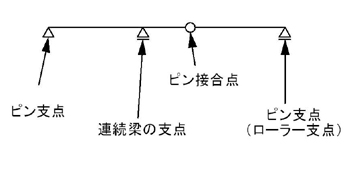
ピン支点,ローラー支点は,単純梁と同様です.部材端部に位置することに注意して下さい.
特徴としては,「反力が生じる」かつ「モーメントは生じない」ことが言えます.
連続梁の支点というのは,部材端部以外にあるピン支点,ローラー支点を指します.
特徴としては,「反力が生じる」かつ「モーメントが生じる」ことが言えます.
ピン接合点というのは,部材端部以外にあるピンを指します(ピン支点ではありません).
特徴としては,支点ではないので「反力は生じない」かつ「モーメントは生じない」ことが言えます.
ポイント1.「ピン支点」「連続梁の支点」「ピン接合点」の違いを理解しよう!
連続梁の問題の解き方は,
ポイント2.ピン接合点(上図C点)のところで切断し,単純梁と片持ち梁として解いていく!
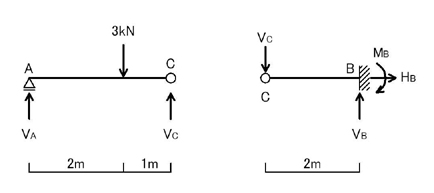
上図のように,まず,ピン接合点(上図C点)で左右に分けて考えます.
左図を単純梁とみなして支点反力を求めます.VA=1kN,VC=2kN(共に上向き)となります.
しかし,C点はピン接合点であり,支点反力は生じないため,上図の右図のC点に下向きのVCを加えてあげることで,C点には支点反力が生じていないことになります.
その結果,VB=2kN(上向き),HB=0,B点での外力系の力の釣り合いを考えると,MB-VC×2=0→MB=2VC=4kN・mとなります.
連続梁は以上のように解くことができます.
それでは,本題に入ります.
「モールの定理(その1)」のインプットのコツのポイント2.で「弾性荷重を考える手順において,支点条件を変更する」ということが必要であると説明しました.
「ピン支点,ローラー支点はそのまま」「固定端は自由端に,自由端は固定端に変更する」わけです.
「モールの定理(その2)」のインプットのコツでは,更に以下の支点条件の変更を考慮することにします.
ポイント3.「連続梁の支点はピン接合点に,ピン接合点は連続梁の支点に変更する!」
モールの定理を用いて問題を解く際の手順は,単純梁や片持ち梁の場合と同様です.
では,具体的に解いていきましょう.
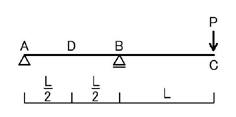
手順1としてモーメント図を描くわけですから,まず最初に支点反力を求めましょう.
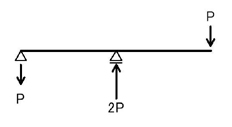
計算は省略しますが,上図のような支点反力が求まります.
そうすると,モーメント図は
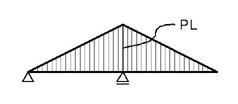
のようになります.
続いて,弾性荷重について考えましょう.
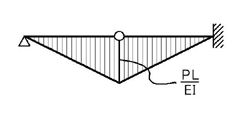
弾性荷重の最大値は,モーメント図の最大値PLをEIで割ったPL/EIとなりますね.また,A点のピン支点の変更はないのですが,B点の連続梁の支点はピン接合点に,C点の自由端は固定端に変更することを忘れないでください.
上図のような荷重が加わったときのC点,D点のモーメントMC,MDがδC,δDとなるので,上図のような弾性荷重が加わったときの支点反力を求めましょう.
三角形荷重を等価な集中荷重に置き換えて考えましょう.
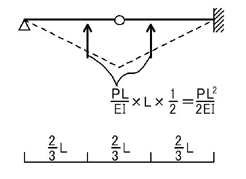
上図のような集中荷重に置き換えることができますね.次に,B点のピン接合点で,単純梁と片持ち梁の2つに分解して考えましょう.
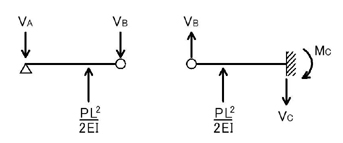
上図のように2つに分解すると,

となり,C点のたわみδCが求まります.続いて,D点のたわみδDを求めましょう.
D点のモーメントMDを求めればいいのでね.下図の三角形荷重を等価な集中荷重に置き換えてみましょう.
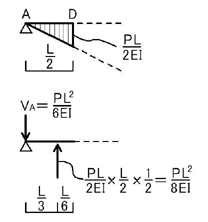
上図のようになることがわかると思います.
よってMDは
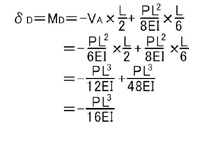
となり,δDが求まります.
ここで気づいた人もいるかもしれませんが,δCは「たわみ」の問題コード14061の問題でした.
新問対策として,少し類題を解いてみましょう.
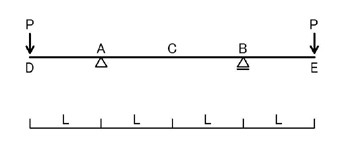
の問題を考えて見ましょう.C点とD点(E点)のたわみを求めてみましょう.
まずは支点反力を考えます.

左右対称であるため,上図のようになりますよね.
で,次にモーメント図を考えましょう.下図のようになりますね.
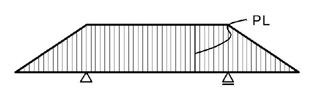
次に,弾性荷重を考えましょう.
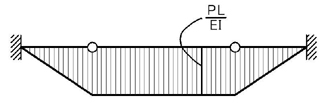
支点の変更はOKですか?
この弾性荷重が加わったときのMC,MDを求めるわけですから,まずは支点反力を求めましょう.
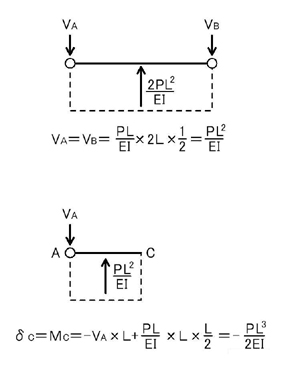
以上により,δCは求まりますね.
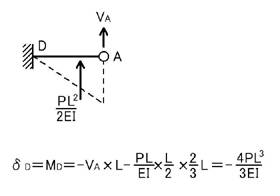
により,δD(=δE)も求まります.
クドイですが,もう一問いきましょう.
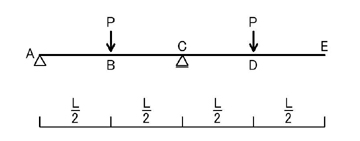
の問題において,E点のたわみδEを求めてみましょう.
以下の説明は,ポイントの抜粋にしますね.各自で解いてみてください.
モーメント図は
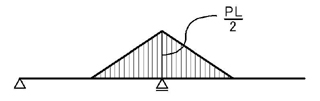
となります.よって,支点の変更に注意して,弾性荷重を考えると
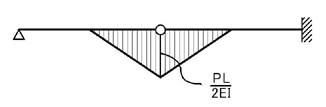
となります.単純梁と片持ち梁に分解すると,単純梁の支点反力は
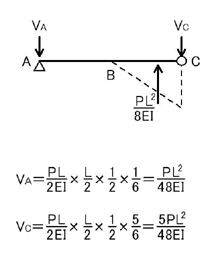
となるため,片持ち梁の先端(C点)に上向きにVCを与えてあげると
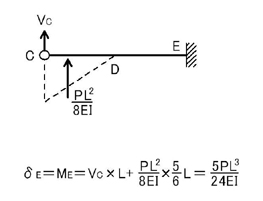
となり,δEが求まりますね.
ここで,「モールの定理」の元になっている考え方に関して説明します.たわみ曲線の微分方程式のことなんですが,「ビ,ビ,ビブン方程式~!?」っていう反応を示す人が多いと思うので,ここでは,結論のみ記載します.詳細を知りたい人は,力学の教科書を見て下さいね.
で,まず最初になぜここで「たわみ曲線の微分方程式」について書くのかについて説明します.
「たわみ」のインプットのコツにおいて,ポイント1.として「たわみ」「回転角」の基本形は覚えよう!という説明をしました.これは,微分・積分アレルギーの人が非常に多いため,最小限の暗記項目で乗り切ろう!という方向性からの説明です.しかし,簡単な微分・積分の計算をすることはOKなので,できるだけ暗記項目を減らしたいという人もいます.文章問題(計画,構造,施工)で暗記することが非常に多いため,この意見も十分理解できます.そこで,たわみと回転角については,「基本形」に関しても計算で行う方法を説明します.
勿論,微分・積分アレルギーの人は,以下の説明については見なくてもいいですよ.
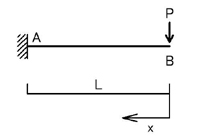
上図の片持ち梁で説明します.
B点から任意の点x(B点からの距離がxである点)でのモーメントMxは,Mx=Pxとなります.
ここで,任意の点(B点から距離xである点)の回転角θは以下の式で表すことができます(結果のみ示します).

任意の点(B点から距離xである点)のたわみδは以下の式で表すことができます(結果のみ示します).

よって,片持ち梁の先端(B点)のたわみ,回転角は(上記式において,x=0とすると)
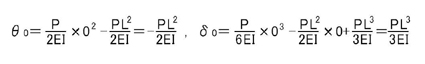
となり,片持ち梁の中央部分のたわみ,回転角は(上記式において,x=L/2とすると)
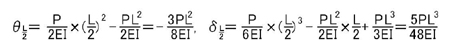
となります.
当然,「たわみ」のインプットのコツのポイント1.「たわみ」「回転角」の基本形に関しても,上記計算で求めることができます.
最後になりますが,外力が集中荷重ではなく,等分布荷重の場合にモールの定理を用いて計算することは得策ではありません.考え方としては,モールの定理で計算することができるのですが,弾性荷重を考える際に,集中荷重の場合は三角形荷重となるため等価な集中荷重に置き換えることがやりやすいのですが,等分布荷重の場合は難しいからです.
もし,等分布荷重の時は
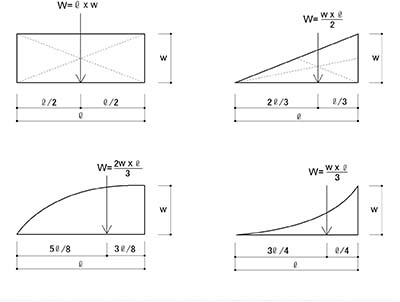
の下側(上側は集中荷重の時)を参考にしてください.
等分布荷重の場合には,上記で説明した「たわみ曲線の微分方程式」で求めることもできます.
また,建築士試験の場合は記述式の試験ではなく,4択の選択式の試験であるため,等分布荷重がかかった問題の場合には,まずモーメント図を描いて,弾性荷重を考えるときに,ほぼ同値とみなせる集中荷重に変換することで,モールの定理を用いて,等分布荷重がかかるときのたわみの近似値を求めることもできます.
しかし,これは最後の悪あがきとしての考え方の一つであると考えてください.






