08.座屈
「座屈」項目の重要ポイントは3つあります.
この重要ポイントを理解すれば,得点源になります.頑張りましょう.
まず最初に「座屈」項目に関して,「現象を数式化し,関係式を導き出す」ことを行ってみましょう.

上図左のように,部材に外力Pが加わる場合について考えてみると,外力Pの値を徐々に大きくしていくと,部材は圧縮されるため上図右のように変形していきます.
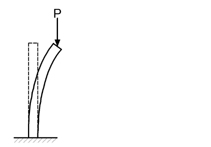
更に,外力Pの値を増やし続けると,ある値を境に部材は上図のように急激に変形してしまいます.この現象を「座屈」といい,座屈に至る時の外力Pの値を「座屈荷重」と呼びます.
次に,「座屈長さLk」について考えて見ましょう.
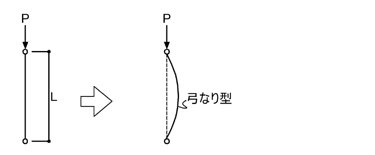
上図のような部材の支持条件を「両端ピン」といい,座屈に至る時の変形は右図のようになります.この時,弓なり型を形成する部分の元の長さを「座屈長さ」と言います.
上図より,「両端ピン」の場合の座屈長さLkは,Lk=Lとなります.
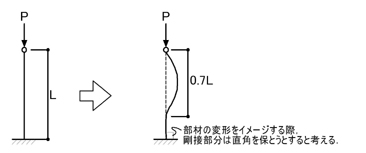
上図のような部材の支持条件を「一端ピン他端固定(水平拘束)」といい,座屈に至る時の変形は右図のようになります.
上図より,「一端ピン他端固定(水平拘束)」の場合の座屈長さLkは,Lk=0.7Lとなります.
なお,何故Lk=0.6LでなくLk=0.7Lなんだろう?とは考えず,ここでは,「一端ピン他端固定」の場合の座屈長さLkは,Lk=0.7Lと覚えてしまいましょう.
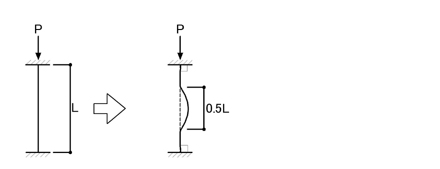
上図のような部材の支持条件を「両端固定(水平拘束)」といい,座屈に至る時の変形は右図のようになります.弓なり型を形成する部分は,元の長さの半分になるため,「両端固定(水平拘束)」の座屈長さLkは,Lk=0.5Lとなります.
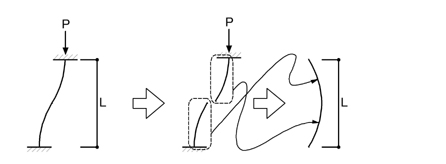
また,上図のように「両端固定」でも水平拘束でない場合の座屈長さLkは,Lk=Lとなります.右図の変形の形を見れば納得できると思います.
以上のことをまとめると
ポイント1.「座屈長さLkは,Lk=0.5L,0.7L,L,2Lの4種類あります」
それぞれの弓なり型が,自分で導けるようにしておいて下さい.
ポイント2.「座屈荷重Pkは,Pk=π^2×EI/Lk^2である」
ここで,Eはヤング係数,Iは弱軸に関する断面2次モーメント,Lkは座屈長さのことです.
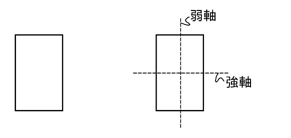
また,弱軸とは,断面2次モーメントが最小になる軸のことです.断面2次モーメントに関しては「断面」のインプットのコツのポイント2.を参照して下さい.
何故,強軸ではなく,弱軸なのでしょうか?
強軸とは変形し難い方向の基準軸,弱軸とは変形し易い方向の基準軸のことを指します.今回のインプットのコツの最初の部分に書きましたが,上から二番目の図で,急激に変形する場合は,変形し難い方向に変形するか,変形し易い方向に変形するかを考えれば,「座屈荷重」を計算する時に用いる断面2次モーメントは「弱軸に関する断面2次モーメント」であることが理解できるかと思います.
座屈荷重Pkは,細長比λを用いて,Pk=π^2×EA/λ^2と表すこともできます(式の変形に関しては,アプリ内解説集の07「座屈の解説のP3を参照して下さい).
つまり,Pk=π^2×EI/Lk^2=π^2×EA/λ^2と書くことができます.
一見すると,座屈荷重Pkは,部材の断面積Aに比例するように見えますが,分母にある細長比λの中に断面積Aは影響しているため,結果的には
ポイント3.「座屈荷重Pkは,部材の断面積Aに比例しない」
ということが言えます.ここまで理解できれば,「座屈」項目に関しては,ほぼ網羅したことになります.
過去問を一読してみましょう.
その時に,「合格ロケット」の解説で,上記重要ポイントを具体的にどのように使っているか!に着眼点を置くことを忘れないでくださいね.
最後に問題コード19061,02061に関して補足説明させていただたきます.
この問題は,18061,29061とは異なり,『梁は剛梁』ではありません(問題文に,「梁は剛体・・・」などと書いていないため).
よって,梁には「曲げ変形」が生じてしまいます.
もし,梁が剛梁で,梁に「曲げ変形」が生じない場合は
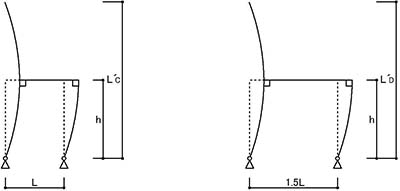
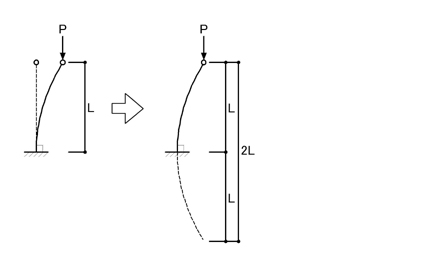
のような全体変形となりますが,梁に「曲げ変形」が生じる場合は
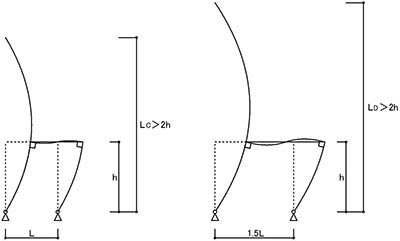
のように,梁端部と柱頭部は「剛接合(直角)」であるため,柱の座屈長さ(=弓なり長さ)は,梁が剛梁の場合より長くなります.
そのことに注意してください.
■ 学習のポイント
この「座屈」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.






