05構造(力学計算編)
01-2.M図の描き方
「単純梁や片持ち梁のM図は描けるのですが,門型ラーメンになるとM図が描けない」という話をよく聞きます.話をよく聞くと「M図が描けない」のではなく「M図を間違える」んですね.
N図,Q図に関しては,部材の上に描くのか下に描くのかは重要ではなく,符号が重要です.一般的には,部材の上側や外側にプラス側を描くことが多いですが.
M図に関しては,符号は重要ではなく「部材の引張側に描く」わけです.
そこで,M図の描き方について勉強してみましょう.単純梁を例にとってM図の描き方の基本的な考え方を説明します.
下の図のような単純梁を考えます.
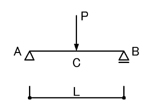
単純梁の場合は,モーメント図が下図のようになるのが納得できる人は多いと思います.
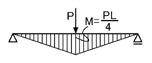
単純梁が下側に引張になり,部材中央のモーメントの値がPL/4になるため,上図のM図が正しいとわかるわけですよね.
それを,もう少し紐解いてみましょう.
外力として集中荷重Pが単純梁の中央に加わっていますので,支点反力は
それを,もう少し紐解いてみましょう.
外力として集中荷重Pが単純梁の中央に加わっていますので,支点反力は
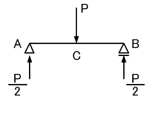
のようになるのはわかりますよね.
■学習のポイント
ポイント1.「M図において,外力が加わっていない部材間のモーメントは直線になる!」
例えば,一番上の図のような単純梁において,A-C間やC-B間には外力が加わっていないため,M図は直線になっていますよね.
よってM図を描く際には,M図の線が折れ曲がる点=外力(支点反力も含む)が加わる点におけるモーメントの値と,部材のどっち側が引張になるかについて注意を払えばよいということがわかります.
例えば,一番上の図のような単純梁において,A-C間やC-B間には外力が加わっていないため,M図は直線になっていますよね.
よってM図を描く際には,M図の線が折れ曲がる点=外力(支点反力も含む)が加わる点におけるモーメントの値と,部材のどっち側が引張になるかについて注意を払えばよいということがわかります.
ポイント2.「ピン支点,ローラー支点にモーメント荷重が加わっていない限り,ピン支点,ローラー支点のモーメントはゼロである!」
これは,00-3「力」の解説②の「反力の種類」を参照してください.
以上により,上記図において,A点のモーメントはゼロであることがわかります.
次に,C点に集中荷重Pが加わっていますので,C点のモーメントを求めましょう.
C点をA側(左側)から見た場合について考えましょう.C点をA側からみた場合のC点のモーメントをMCAと表現することとします.
C点をA側(左側)から見るわけですから,下図のように,C点の右側を無視することとします.
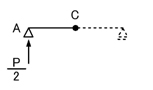
A点に支点反力として,上向きP/2の力がありますので,C点のモーメントMCAはMCA=+P/2×L/2=+PL/4となります.
C点の左側には+PL/4(+であるため,時計まわりのモーメントであることがわかります)のMCAが生じているため,「内力系の力の釣り合い(作用・反作用)」よりC点の右側には-PL/4のモーメントが生じていることがわかります.
C点の左側には+PL/4(+であるため,時計まわりのモーメントであることがわかります)のMCAが生じているため,「内力系の力の釣り合い(作用・反作用)」よりC点の右側には-PL/4のモーメントが生じていることがわかります.
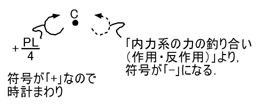
下図の左図のように,C点の左側には時計まわりの,右側には反時計まわりのモーメントが生じているので,C点は下図の右図のような下側が引張になるような変形をすることがわかります.
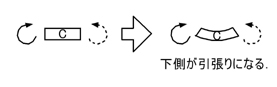
つまり,単純梁の部材中央に集中荷重Pが加わる場合には,下側にモーメント図を描くわけです.
上記の説明は理解できましたでしょうか.
複雑な形状の問題も,上記考え方でM図は間違えずに描けるようになります.
Q図に関しては,00-8「M図,Q図のイメージ」の解説の「Q図変換」の考え方を用いると,M図からQ図がすぐ求まると思います.
複雑な形状の問題も,上記考え方でM図は間違えずに描けるようになります.
Q図に関しては,00-8「M図,Q図のイメージ」の解説の「Q図変換」の考え方を用いると,M図からQ図がすぐ求まると思います.






