02.断面の性質
この項目の重要ポイントは3つあります.
ポイント1.断面1次モーメント(S)
・02「断面の性質」の解説に目を通してください.考えの基本は,矩形(四角形)の図心位置の求め方です.
・断面1次モーメントは,「足し算・引き算」が可能であることを利用して,L型やT型の図心位置を求めることができるようになってください.
ポイント2.断面2次モーメント(I)
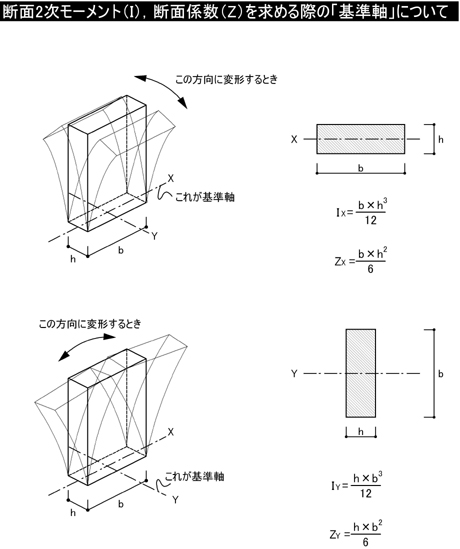
・これは,部材の変形のしにくさを表します.02「断面の性質」の解説にあるように,図心を通る基準軸に関する断面2次モーメントIxがIx=b×h^3/12であることは暗記してしまいましょう.
・「どの軸」に対する断面2次モーメントであるのかに注目してください.
・「足し算・引き算」が可能であるため,□型やI型断面の断面2次モーメントは,分割したそれぞれの図形の断面2次モーメントの和(や差)になることを理解しましょう.
ポイント3.断面係数(Z)
・これは,曲げ強さを表します.図心を通る軸についての断面2次モーメントを図心軸から断面縁までの距離で割って求めることが出来ます.矩形(四角形)の図心を通る基準軸に関する断面係数ZはZ=Ix/(h/2)=b×h^2/6となることを理解しましょう.
・「どの軸」に対する断面係数であるのかに注目してください.
・注意ポイントは,断面係数は「足し算・引き算」が不可能であるため,□型やI型断面の断面係数を求める際には,「□型やI型断面の断面2次モーメント」を計算して,図心軸(基準軸)から縁までの長さで割って計算することを理解しましょう.
・この考えは,03「応力度」の問題などで必要になるために,ここの単元で理解しておきましょう.
補足
断面2次半径(i),断面極2次モーメント(Ip),断面相乗モーメント(Ixy)に関しては,02-1「断面の性質」の解説を一読しておいてください.基本的事項(定義)を覚えておきましょう.
また,「基準軸」という概念を強くイメージしてください.
■学習のポイント
この「断面の性質」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.問題コード18011では,梁A,B,Cがどのように変形するかについてイメージできれば正答肢にたどり着けると思います.特に梁Cに関して変形をイメージできたかがポイントとなりました.
梁Cの変形は,3つのうちの中央部材の中心軸に関して,上部材や下部材が変形するのでしょうか?
上部材は,上部材の中心軸に関して変形しますよね?同様に,下部材は,下部材の中心軸に関して変形しますよね?
この点に着目して,18011を解いてみましょう.
その他の問題については,H型やロ型などの矩形(長方形)以外の断面二次モーメントや断面係数を求めることができるようになっておきましょう!
なお,知っておくと便利な関係として,一辺の長さがDである正方形の断面二次モーメントI□=D^4/12と,直径がDである円の断面二次モーメントI○=πD^4/64の関係として,
I○≒0.6×I□ の関係です.
この関係を知っていると,円の断面二次モーメントの公式を忘れても,大体の大きさを計算することができます.






