03.応力度
「応力度」の重要ポイントの説明をする前に,「力」について説明させていただきます.
まず最初に,00-3「力」の解説②~00-6「力の流れ」の解説(補足編)までを一読して下さい.
そうすると,「力」には「外力」と「内力(応力)」という2つの種類があることを理解できると思います.
「外力」とは,物体の外から加わる力のことです.具体的に言えば,例えば単純梁に加わる集中荷重Pや,支点反力などを指します.
一方,「内力」とは,外力によって物体内部に生じる力のことです.外力に応じて生じる力のため「応力」とも言われます.
言葉を変えれば,「外力」が一切加えられなければ(重力なども含む),「内力」は生じません.
ここで,もう一度,00-5「力の流れ」の解説の「作用・反作用の法則」と「内力伝達のイメージ」の部分を読み返してください.
実は,00-5「力の流れ」の部分は,非常にとっつきにくい部分で,この部分が原因で力学計算に嫌気がさしてしまう人が多いです.
なので,「力の流れ」の解説を読み返してみて嫌気がさしてきた人は,あまり深入りせずに次に進みましょう.
力学計算を一通り勉強した後で読み返してみると,意外とすんなり理解できたりしますので,現時点ではあまり心配しないで下さい.
ここで,なぜ「応力度」の勉強をするのかについて,簡単に説明したいと思います.
実際の構造設計において,「許容応力度計算」というものがあります.
概念を説明すると,地震などの「外力」により,部材内部には「内力(応力)」が生じます.その「応力度」が部材材料ごとに決まっている「許容応力度」より小さければ,その部材は「安全」,大きければ部材断面の変更などをしなければなりません.
そのために「応力度」という概念が必要になってきます.そのための勉強であることに気づけば,少しはやる気が起きるかもしれませんね.
「応力」と「応力度」について
「応力度」とは「応力」の「密度」のことを指します.よって,軸方向力が加わった時のように,ある面に一様に「内力(応力)」が生じた場合に部材中の各点に生じる応力度は,「外力」をその点の断面積で割ったものになります(軸方向力なので「垂直応力度」といいます).
生じる「内力」が曲げモーメントやせん断力の場合は,ある面に一様に「内力(応力)」が生じるわけではないので,「垂直応力度」のように「内力(応力)」を断面積で割っただけでは「応力度」は求まりません.
これらについては,以下に挙げる重要ポイントの中で説明させていただきます.
まずは,03-1「応力度」の解説を一読してください.
この項目の重要ポイントは3つあります.
ポイント1.垂直応力度σ(シグマ)
・これは外力により,部材内部に生じる部材方向の「内力(応力)」に関する「応力度」であるため,
垂直応力度(σ)=軸方向力(N)/断面積(A)となります.
ポイント2.せん断応力度τ(タウ)
・これは外力により,部材内部に生じる部材と直交方向「内力(応力)」に関する「応力度」であるため,
平均せん断応力度(τ)=せん断力(Q)/断面積(A)となります.
・せん断応力度(τ)は,垂直応力度(σ)と異なり,応力度は部材断面内に一様に発生しません.矩形断面(四角形断面)や円形断面におけるせん断応力度の分布は断面の中央部が最大となり,縁の部分ではゼロとなります.
・矩形断面における最大せん断応力度(τ)はτ=3/2×Q/A,円形断面における最大せん断応力度(τ)はτ=4/3×Q/Aとなります.
ポイント3.曲げ応力度σb(シグマビー)
・曲げモーメントを受ける部材は,中立軸を境に圧縮側,引張側に分かれます.曲げ応力度は中立軸上でゼロとなり,中立軸から遠ざかるほど大きくなるため,部材断面上下縁で最大となります.これを「縁応力度」と呼び,「曲げ応力度」とは基本的に「縁応力度」のことを指すため,曲げ応力度(σb)=曲げモーメント(M)/断面係数(Z)となります.
・なぜ,曲げモーメントを断面係数で割ると曲げ応力度になるのかは,「全塑性モーメント」のインプットのコツの中で解説させていただきますので,現時点では,そのまま覚えてしまいましょう.
断面内部に生じる「応力度」をすべて足すと,外力によって生じる軸方向力・せん断力,曲げモーメントなどの「応力」になります.
言葉を変えると,軸方向力・せん断力,曲げモーメントなどの「応力」を面積あたりに分解すると「応力度」になります.
これら3つの重要ポイントに注意を払い,過去問題を解いてみましょう.
このように「現象を数式化し,関係式を導き出す」ことが,力学計算編を得点源にする最大の要因の一つであることを理解してください.
次に,過去に出題されたことのある2軸曲げについて,補足説明させていだたきます.
偏心荷重という言葉を聞いたことがありますか? 偏心荷重とは,
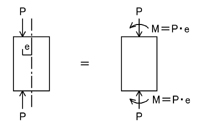
のように,部材には外力として軸方向力である集中荷重Pしか加わっていないのに,外力の加わっている位置によって,部材には集中荷重Pの他に,集中荷重Pによって生じる曲げモーメントも同時に外力と加わっているとみなせるような集中荷重Pを指します.
上記左右の図に生じる内力(応力)が同じものになる,言葉を変えれば,左右の図が=で結ばれることが理解できるようになればしめたものです.
この問題は,「2軸曲げの問題」といい,「応力度」の問題の中では最も難しい問題です.部材の端部に外力Pが加わることにより,ニ方向に変形が進む(3次元的変形)問題だからです.
余り深入りせず(現時点で理解できなくてもいい難しい問題です),一通り勉強が終わった際に,余裕があれば見直せばよい問題(通称:捨て問)の一つです.
2軸まげの問題を捨てない人のために,補足説明を続けますが,
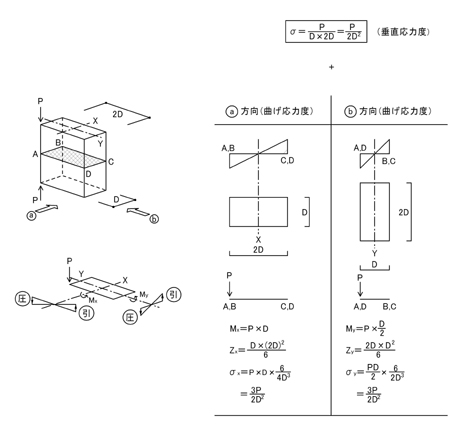
a方向から見た場合,外力Pによって断面の左側(A点,B点側)が圧縮,断面の右側(C点,D点側)が引張になります.同様に考えると,b方向から見た場合,外力Pによって左側(A点,D点側)が圧縮,断面の右側(B点,C点側)が引張になることがわかります.
以上より,圧縮応力度をマイナス,引張応力度をプラスとした場合,A点からD点のうち,A点に生じる応力度が最も小さく(a方向から見てもb方向から見ても圧縮側なので),C点に生じる応力が最も大きく(a方向から見てもb方向から見ても引張側なので)なると判断することができます.
各点に生じる応力度の具体的な値は上記ポイント1.とポイント3.より計算できます.
この「応力度」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.






