04.全塑性モーメント
部材に曲げモーメントMのみがかかる場合の,部材内部の「応力」状態を見ていきましょう.
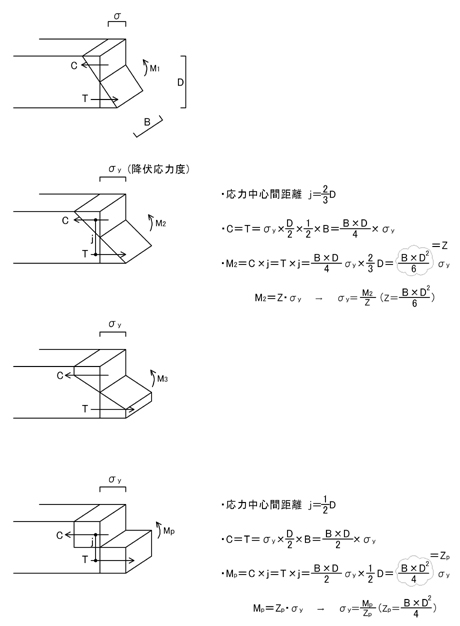
これは,「微小変形理論」や「平面保持の仮定」というものに基づいているからなんですが,こんな言葉「微小・・・」などは知らなくてもいいです.部材中央に曲げモーメントMを受ける場合,圧縮側の縁応力度も引張側の縁応力度も同じ大きさになることは感覚的に理解できると思います.
この曲げモーメントが少しずつ大きくなると,圧縮側,引張側共に,縁応力度が降伏応力度σy(部材材料ごとによって異なります)に達します(上記図の二番目の図).ココまでが弾性範囲です.
降伏応力度σyとは,部材材料が降伏する(壊れてしまう)応力度であるため,更に曲げモーメントMが大きくなると,三角形(三角柱)の応力状態を保てなくなります.上記図の三番目の図のように,台形のように応力状態が進んでいきます.更に曲げモーメントMが大きくなると,上記図の一番下の図のようになります.これ以上は増えようがないので,上記図の一番下の図のような応力状態を「塑性状態」といい,塑性ヒンジが生じることになります.塑性ヒンジに関しては,「崩壊荷重」のところで説明します.
ここで,00-3「力」の解説②「モーメントって何?」「モーメントの計算」,00-5「力の流れ」の解説の「力の発生のイメージ」を一読して下さい.
つまり,「モーメント」とは,「大きさが同じ」で「向きが逆」の一対の集中荷重(「偶力」と言います)に置き換えて考えることが出来ます.
もう少し具体的な例で説明しますと,自動車の運転の「ハンドル」や水道の「蛇口」を思い出してください.
自動車の運転で右折する際には,ハンドルを時計廻りに回します.実際には,左腕を上に,右腕を下に動かすことで,ハンドルは時計廻りに回ります.
曲げモーメントM2を受ける部材(上記図の上から二番目)でも,同様に,曲げモーメントM2を圧縮合力Cと引張合力Tという,「大きさ同じ」で「向きが逆」の一対の力(偶力)で置き換えて考えることができます.
弾性範囲内で考えた場合,圧縮合力Cや引張合力Tの大きさは,三角柱の体積に相当します.よって,C=T=σy×D/2×1/2×Bとなることが理解できるかと思います.
偶力の距離(応力中心間距離といいます)をjとすると,M=C×j=T×jとなるため(これは,00-5「力の流れ」の解説の「力の発生のイメージ」参照),上記図の二番目の図横に書いてあるように,M2=B×D^2/6×σyとなります.
「応力度」のインプットのコツで,曲げ応力度σbとは,曲げモーメントによって生じる「応力度」であるため,σb(σy)=M2/(B×D^2/6)となっていましたよね.σb=M/Zと比較すると,Z=B×D^2/6となることが理解できると思います.
塑性状態(上記図の一番下の図)の場合,圧縮側,引張側ともに応力状態は三角形(三角柱)ではなく四角形(四角柱)になるため,圧縮合力C,引張合力Tはともに,上記図の一番下の図横に書いてあるように,C=T=σy×D/2×B=B×D/2×σyとなります.これら偶力の距離jは,j=D/2となります(これは,上記図の一番下の図より理解できますよね).
塑性状態の時のモーメントを全塑性モーメントといい,Mpと記すとします.そうすると,Mp=C×j=T×j=B×D/2×σy×D/2=B×D^2/4×σy・・・①と計算できます.
部材断面が塑性状態であるときの断面係数を塑性断面係数Zpと記すと,弾性状態の時と同様に,Mp=Zp×σy・・・②と表すことができます.
①と②式を比較すると,Zp=B×D^2/4となります.これは,覚えてしまいましょう.
この項目の重要ポイントは2つあります.
ポイント1.塑性断面係数Zpは足し算・引き算が可能である.
「断面の性質」のインプットのコツで説明しましたが,弾性状態の断面係数Zは,足し算・引き算できません.でも,塑性断面係数は足し算・引き算が出来ます.これは,覚えてしまいましょう.
ポイント2.部材に曲げモーメントMと軸力Nの両方がかかる場合の解き方です.
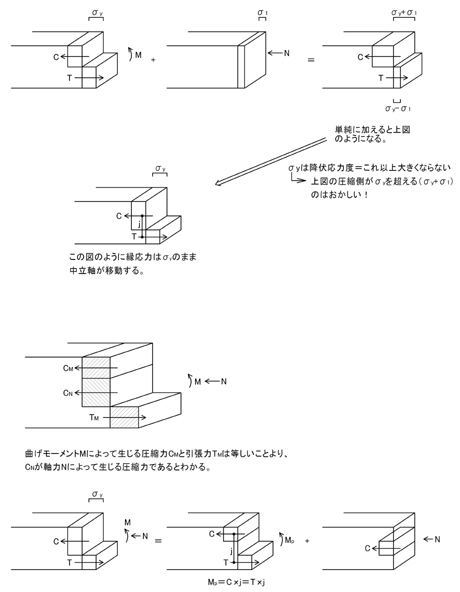
部材に曲げモーメントMと軸力Nの両方がかかる場合には,上の図の上段に並んでいる3つの図の右側のように縁応力がσyを超えるような応力状態は起きずに,実際は,その下の図のように,縁応力はσyのまま,中立軸(圧縮領域と引張領域の切り替わる部分)が移動します.
言葉を変えると,縁応力はσyを超えることができないので,上記上から2段めの図のように,曲げモーメントMと圧縮軸力Nが両方かかる場合は,圧縮側の応力場(四角柱の体積)が大きくなるわけです.
曲げモーメントは偶力で表すことができましたよね.偶力とは,「大きさが同じ」で「向きが逆」の一対の集中荷重であるため,曲げモーメントMによって生じた圧縮合力CMと引張合力TMは同じ大きさになります.
残りの圧縮合力が軸力Nによって生じた圧縮合力CNと考えることができます.
まずは,基本となる矩形断面の24011で,「基本的な問題の解き方」をマスターしてしまいましょう.
その次には,22011,02011,25011のようなH型や,28011,30011のようなロ型をマスターしていきましょう!
■学習のポイント
この「全塑性モーメント」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるので,得点源にしてしまいましょう!






