05.崩壊荷重
この項目に対して「難しそう・・・」というイメージを持っている人が多く見られます.が,実は,得点源の項目です.
以下に説明する重要ポイントを理解すれば,得点源になります.頑張りましょう!
まず最初に,言葉の説明をします.
・崩壊:単純梁やラーメンなどの構造物に荷重を作用させ,その大きさを増大させていく時,それ以上の荷重を加えなくても「ただ変位のみが増大して」変形を生じる状態
・崩壊荷重:崩壊の生じる時の荷重
・崩壊機構:構造物に塑性ヒンジが形成され,その構造物が不安定な状態になるメカニズム(機構)
・塑性ヒンジ:部材のある断面が全塑性モーメントに達して,回転自由なピン状態になった部分
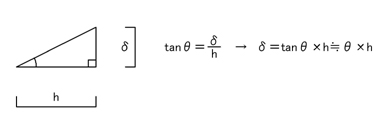
次に,『学科試験の「崩壊荷重」の問題を考える時の回転角θはすごく小さい時を考える』という前提条件に基づいていることを覚えておきましょう.それによって,回転角θがすごく小さい時は,tanθ≒θとみなすことができるんです.このことも覚えておいて下さい.
ここで,「合格ロケット」に収録されている05-1「崩壊荷重」の解説を一読して下さい.
この項目の重要ポイントは5つあります.
ポイント2.仕事(量)=力×移動距離
単純梁やラーメンなどの構造物に外力Pを加えていくと,構造物に内力が生じます.外力が増えるにつれ,内力も増えていきます.一番弱い部材が塑性状態になります(塑性ヒンジが発生します).
具体的な問題の解き方は,「外力による仕事」と「内力による仕事」が等しいという点に着目します.
「外力による仕事」とは,外力Pによって,材が変形します.その仕事量(=力×移動距離)を指します.
「内力による仕事」とは,外力Pによって,材に内力が生じます.構造物が崩壊機構に達した時に,部材に塑性ヒンジが発生して,部材が回転します.その仕事量(=部材の塑性モーメント×回転角)を指します.
ポイント3.塑性ヒンジは部材の弱い方に発生します.
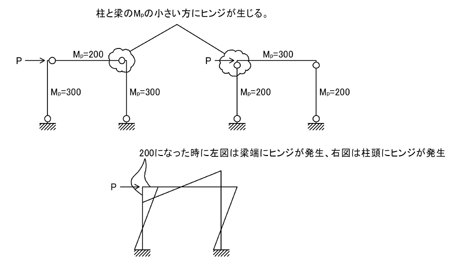
上記左図では,梁の塑性モーメントが200,柱の塑性モーメントが300であるため,外力Pによって柱と梁に生じる内力(曲げモーメント)が200に達した時点で,柱ではなく梁の方に塑性ヒンジが発生します.
ポイント4.柱の長さが異なるラーメン構造物の「外力」による柱の移動距離の求め方
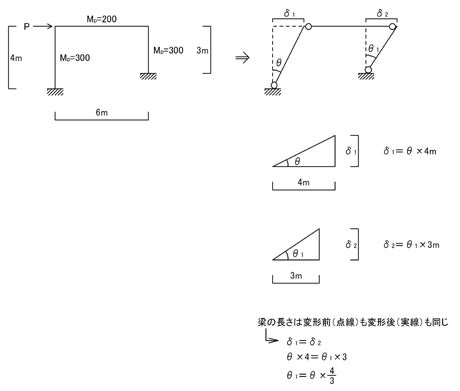
ポイントは,梁の長さは,変形前も変形後も変化しないことです.
ポイント5.「内力による仕事(=部材の塑性モーメント×回転角)」は『新たに発生したヒンジに関してのみ』考慮すること
例えば,片側が固定端,もう一方がピン支点であるラーメン構造物の場合,ピン支点の部分に関しては,元々ピンであり,塑性ヒンジが発生したわけではないので,「内力による仕事」とは考えません.
以上の重要ポイントに意識して,過去問を解いて見ましょう.
■ 学習のポイント
一番最初の部分に書きましたが,この「崩壊荷重」という項目に苦手意識を持っている人は多いのですが,意外と点数が取りやすいと思えるようになりませんか?もう一度,解説に目を通してください.
この「崩壊荷重」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットアプリに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できますよ!






