07-1.モールの定理(その1)
単純梁や片持ち梁に集中荷重やモーメント荷重が加わるときの部材の「たわみ」や「回転角(たわみ角)」を求める方法に「モールの定理」があります.
「モールの定理(その1)」のインプットのコツでは,まず最初に,単純梁と片持ち梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法を説明します.
「モールの定理(その2)」のインプットのコツでは,部材端部以外に支点がある架構や連続梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法を説明します.続いて,「モールの定理の元になっている考え方」他に関して説明します.
「モールの定理」の基本として,
ポイント1.「各点の回転角は,弾性荷重によるその点のせん断力Qに等しい」「各点のたわみは,弾性荷重によるその点のモーメントMに等しい」
ポイント2.「ピン支点,ローラー支点はそのまま」「固定端は自由端に,自由端は固定端に変更する」
があります.
ここで,「弾性荷重」とは,(梁に生じる)曲げモーメントMを,その梁の曲げ剛性EIで割ったM/EIのことを指します.
言葉だけではイメージし難いので,具体例を用いて説明していきましょう.
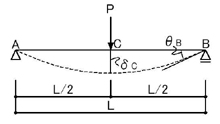
上図のような単純梁のC点におけるたわみδC,B点における回転角θB(A点における回転角θA)を求めてみましょう.
手順1.M図を求めます.M図は下図のようになりますね.
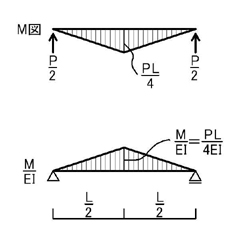
手順2.上図のように,部材中の各点に発生する曲げモーメントMをEIで割った数値をM図が発生する側と逆側に荷重(弾性荷重)として作用させます.
この時に,ポイント2.に注意しましょう.上図の問題では,単純梁であるため,ピン支点とローラー支点しかないため,支点の変更はありません.
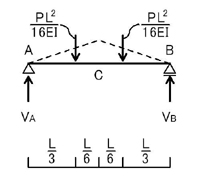
外力系の釣り合いは上図のようになるため,支点反力VA=VB=PL^2/16EIとなります.
よって,A点における回転角θA,B点における回転角θB,C点におけるたわみδCは
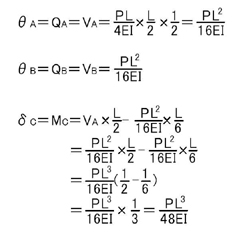
続いて,片持ち梁の先端に集中荷重が加わるときについて考えて見ましょう.
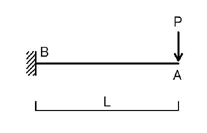
のような場合ですね.
手順は単純梁の場合と同様です.
M図は下図のようになりますね.
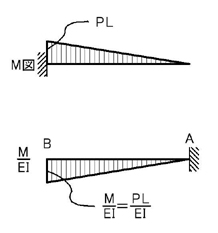
MをEIで割った弾性荷重を作用させた場合を考えて見ましょう.
ポイント2.に注意しましょう.「固定端は自由端に,自由端は固定端に変更する」とは,具体的には上図のように,弾性荷重を考えるときに,支点の状態を変更して考えることを指します.
この三角形の弾性荷重は,
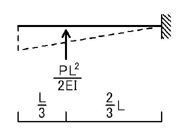
のように,集中荷重に置き換えて考えて見ましょう.重心位置に三角形の面積分の荷重がかかると考えればいいのです.
そうすると,A点の回転角θA,B点の回転角θB,A点のたわみδAは

のようになります.問題の図において,B点は固定端であるため,B点の回転角はゼロになるのは理解できますね.
続いて,下図のように,片持ち梁の(先端以外の)ある点に集中荷重が加わるときについて考えて見ましょう.
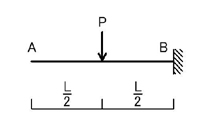
M図は下図のようになります.
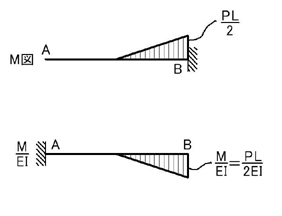
弾性荷重を考えると上図のようになることがわかると思います(支点の変更に注意!).
下図のように,三角形荷重を集中荷重に置き換えて考えると
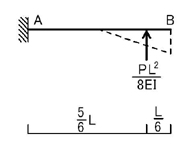
A点,B点の回転角とA点のたわみは
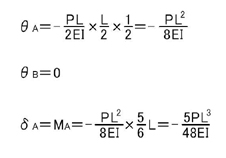
のようになります.
続いて,モーメント荷重が加わるときについて考えて見ましょう.
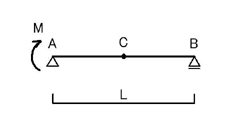
上図のような問題ですね.
モーメント荷重が加わる場合の考え方は,集中荷重が加わるときと同様です.
まずは,モーメント図を考えましょう.
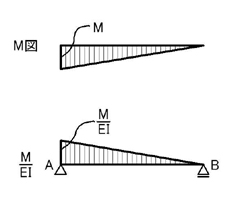
上図のように,弾性荷重を考えます.この問題の場合は,単純梁であるため,ポイント2.の支点の変更はありません.
ポイント1.より,A点,B点のせん断力QA,QBを求める(=支点反力VA,VBと同じ値になります)ことにより,A点とB点の回転角θAとθBが求まります.C点のモーメントの値MCを求めることで,C点のたわみδCが求まります.
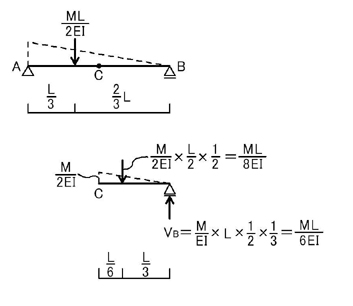
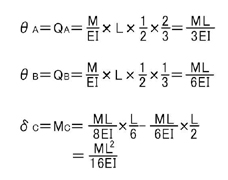
次に,この問題におけるたわみが最大の点のたわみδmaxを求めてみましょう.
δmaxはθ=0の位置であることは理解できるでしょうか.
単純梁の部材中央に集中荷重が加わる場合(このインプットのコツの一番上の図参照)を考えて見ましょう.
部材中央のC点のたわみが最も大きいことは理解できると思います.この図において,端部(A点,B点)の回転角θAとθBが最も大きく,中央部C点の回転角θCはゼロであることがわかるかと思います.
ポイント3.たわみの最大値は,回転角がゼロとなる位置で生じる!
では,単純梁にモーメント荷重が加わる場合のδmaxを求めてみましょう.
下図のように,弾性荷重を考え,B点から任意の点(B点から距離xだけ離れた点をx点とします)でのせん断力Qxを計算します.
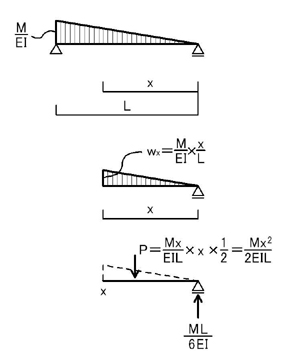
上図のように,x点より右側を考え(左側でも構いません)ます.B点の支点反力は上向きにML/6EI,弾性荷重のうち,今回対象範囲(x点から右側の部分の三角形)を集中荷重に置き換えて考えるとP=Mx^2/2EILとなります.
よって,x点でのせん断力Qxは
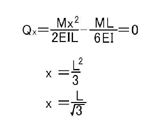
となり,δmaxはB点よりL/√3の位置で生じることがわかります.
下図のような片持ち梁にモーメント荷重が加わるときについてはどうでしょうか.
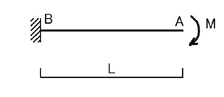
M図は下図のようになり,
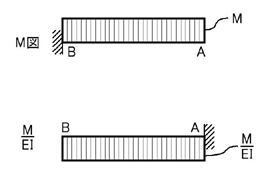
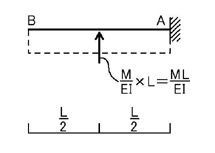
弾性荷重M/EIは上図のようになりますね.
A点でのせん断力QAはM/EIとなり,A点でのモーメントはML^2/2EIとなることが理解していただけると思います.
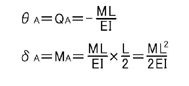
以上の説明は理解できましたでしょうか.
「モールの定理(その1)」のインプットのコツでは,単純梁や片持ち梁に集中荷重,モーメント荷重が加わる場合の「モールの定理」の計算方法について説明しました.
通常のテキストなどでは,「モールの定理」とは,単純梁と片持ち梁を対象とした説明になっていると思われます.しかし,この考え方を拡張すると,架構の中間に支点のある架構にも適用することができます.
それについては「モールの定理(その2)」のインプットのコツで説明します.






