10-1.応答スペクトル
「固有周期」のインプットのコツのポイント2.で説明した固有周期で「固有周期の式のmとkのうち,どっちが分子で,どっちが分母かがわからなくなるのですが・・・」という質問をよく受けます.
同じ剛性kで質量mの1質点系(質量mの重い串団子と軽い串団子)では,どちらの方が周期が長くなるかを考えれば分かり易くなるかと思います.
考え方を逆にすると,同じ質量mで,串の長さが長い串団子と短い串団子では,どちらの方が周期が長くなるでしょうか.
長い串と短い串では,長い串の方が剛性(k)が小さく(軟らかく)なることはイメージできるかと思います.
そうすると,(串の先端にある重りが同じ質量ならば)串の長さの長い方が周期は長くなりますね.
つまり,固有周期の式において,質量mが大きい方が,剛性kが小さい方が,固有周期は長くなることはイメージできるかと思います.
続いて,本題の「応答スペクトル」に関して,説明させていただきます.
「応答スペクトル」には,「加速度応答スペクトル」,「速度応答スペクトル」,「変位応答スペクトル」の3種類があります.
もう,この辺で,拒絶反応を示す人が多いのですが,構造科目で25点以上を狙う人は,我慢してついて来てください.
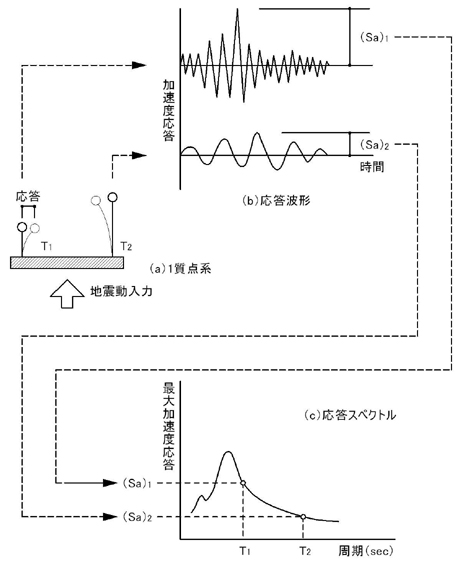
新・地震動のスペクトル解析入門(鹿島出版会)から抜粋(一部修正)
上記図(a)の1質点系の串団子があるとします.この例では,周期T1とT2の2種類を示しています.この周期は何秒でも構いません(ここでは,T1<T2としています).また,串団子の先端質量の大きさが何kgであるかに関しても関係ありません.串団子の先端質量mと剛性kによって定まる固有周期Tが重要なんです.
例えば,先端質量m,剛性kの串団子と,先端質量2m,剛性2kの串団子の固有周期は同じ値になることは理解できますよね.
よって,串団子の先端質量mや剛性kの具体的な数値は,関係ありません.
次に,上記図(a)のように,この串団子を揺らします.
その時の,串団子の先端質量の加速度が上記図(b)になったとします.(a)にある2種類の串団子の周期が異なるため,(b)にあるように,先端質量の加速度波形は異なった形になります.その時の最大の加速度を(Sa)1と(Sa)2とすると,周期T1の串団子の最大加速度(Sa)1,周期T2の串団子の最大加速度(Sa)2,・・・・・・というように,図(横軸:周期T,縦軸:加速度(Sa))にプロットしていくと,上記図(c)のようになります.
上記図では,2種類の串団子の例ですが,これをいろいろな固有周期Tの串団子を揺らして,その固有周期Tと最大加速度Saを図にプロットしたものが,「加速度応答スペクトル」と言います.
同様に,いろいろな固有周期Tの串団子を揺らして,その固有周期Tと最大速度Svを図にプロットしたものが「速度応答スペクトル」,その固有周期Tと最大変位Sdを図にプロットしたものが「変位応答スペクトル」と言います.
この「応答スペクトル」に関しては,一般的な傾向として,
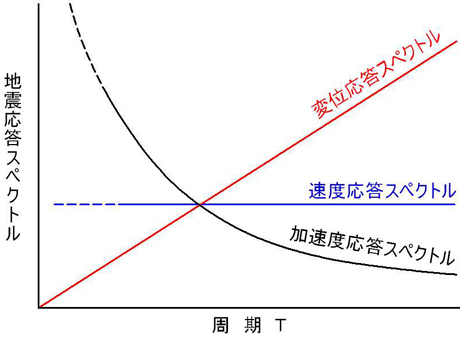
新・地震動のスペクトル解析入門(鹿島出版会)から抜粋(一部修正)
の関係があると言えます.
つまり,
加速度応答スペクトルは,固有周期Tが長くなると,減少する
速度応答スペクトルは,固有周期Tが長くなると,ほぼ一定になる
変位応答スペクトルは,固有周期Tが長くなると,増加する
傾向があると言えます.
これは,構造(文章題編)でも問われている事柄でもありますので,ぜひ覚えてください.
覚え方としては,変位応答スペクトルを考えてみて下さい.
上図(a)のように,固有周期Tがことなる2種類の串団子をイメージします.変位応答スペクトルとは,串団子を揺らした時の先端質量の最大変位をプロットしたものでした.そうすると,上図(a)の固有周期T1とT2のうち(T1<T2とする),どちらの串団子の先端変位が大きいかを考えると,固有周期が長い方(上記図(a)で言えば,T2の方)が変位が大きいことがイメージできると思います.
よって,串団子の棒の長さが長い方=固有周期Tが長い方が応答変位スペクトルは大きくなることが理解できるかと思います.
固有周期Tが長くなれば,速度応答スペクトルは一定,加速度応答スペクトルは小さくなる(変位応答スペクトルと逆)ことを思い出すことができると思います.
建築士の学科試験に関しては,以上のことを知っていれば,十分であると考えます.
「固有周期」項目の問題コード25071について,補足説明させていただきます.
この問題のポイントは,高校の物理で習ったせん断力Q=m×a(m:物体の質量,a:加速度)を思い出せるかです.
質量mに関しては問題で与えられているので,串団子A,B,Cのそれぞれにかかる加速度が,それぞれいくつになるのかを問題の応答加速度スペクトルの図から求めなければなりません.
問題の応答加速度スペクトルの図より,固有周期T1<T2<T3において,固有周期T1の串団子の加速度は0.5g,固有周期T2の串団子の加速度は0.4g,固有周期T3の串団子の加速度は0.3gと読み取れます.
よって,串団子A,串団子B,串団子Cの固有周期がT1,T2,T3のどれかと対応しているので,その関係を求めます.
具体的には,T=√(m/k)より,TB<TA<TCと求められるので,串団子Bにかかる加速度は0.5g,串団子Aにかかる加速度は0.4g,串団子Cにかかる加速度は0.3gとなることがわかります.
よって,Q=m×a(串団子Cの質量のみ2m)より,QA,QB,QCの値が具体的に計算でき,QA<QB<QCとなることがわかります.
問題コード28261に関しても,同様に考えることで答えを求めることができます.
問題コード28261の解説を参照して下さい.






