05.構造計画(構造計算方法)
まずは,オンライン講義の様子をご覧ください(Youtube動画 約6分)
今回のインプットのコツでは,構造計画の中の構造計算方法に関して,概要説明をします.
建築基準法においては,法規科目の「09.構造」にあるように,令81条にて構造計算方法が規定されています.
これらのうち,本来は1項に規定されている超高層用の構造計算(いわゆる,時刻歴応答解析)を行わなければ,柱や梁,壁などに生じる応力が分からないのですが,この構造計算が非常に複雑であるため,高さが60m以下の建築物については「簡易法」で構造計算をしましょう!ということになっています.
その「簡易法」については,令81条の2項及び3項で規定されている保有水平耐力計算以下となります.
「簡易法」とは言え,令81条の2項第一号イで規定されている保有水平耐力計算や,第一号ロで規定されている限界耐力計算については,実はかなり難しい内容となっております.
ですが,一級建築士の学科試験で得点する!ということに着眼点を置くのであれば,構造(文章題編の「05-2.荷重・外力(地震力関係)」に記載されている計算方法の内容と,建築基準法には記載がされておりませんが,構造科目としては出題されている下記の「構造耐震計算ルート」について,重要ポイントをおさえておきましょう!
構造耐震計算では,地震力の強さを2段階で考えています.建築物が耐用年限内に数回遭遇する程度の中地震と,耐用年限内に1度遭遇するかもしれない大地震によるものの2段階です.
中地震については,強度型か靭性型かによって求める層間変形角の具体的な数値は異なりますが,靭性型の建築物であっても,基本的には弾性内の変形である層間変形角が1/200程度以下となるようにして,亀裂などが生じても,軽微な補修で対応が可能であり,仕上げや設備に損傷を与えずに使用上支障がないことを目指します.
一方,大地震については,中地震の2倍程度の塑性変形,靭性型の建築物であっても,層間変形角を1/100~1/150程度以下となるようにして,建築物の倒壊などを防ぎ,人命の保護を図ることを目指します.
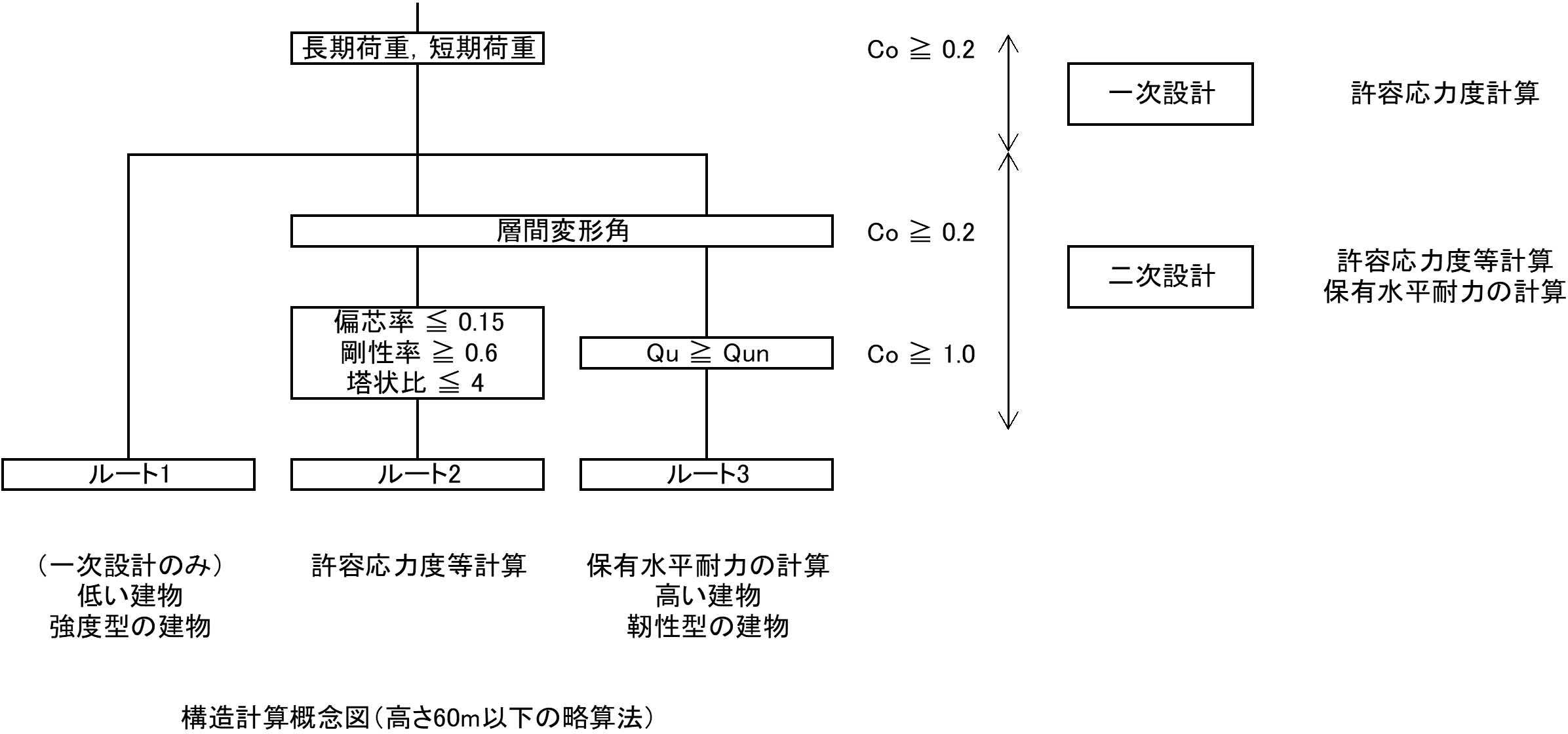
過去問題でも出題されているこれらの構造耐震計算フローにおける「ルート1」とか「ルート2」という言葉は建築基準法では規定されておりませんが,内容については,平成19年国交省告示第593号及び昭和55年建設省告示第1791号により規定されている内容です.
鉄筋コンクリート造や鉄骨造などの構造種別によらず,「一次設計」とは,長期荷重(地球の重力によって生じる荷重)及び短期荷重(中地震などを想定)において,荷重や外力によって各部材に生じる応力度が材料の許容応力度以下になるようにして,損傷防止の確認を行うことです.
具体的には,令82条で規定されている許容応力度の計算を行い,使用上の支障防止の確認,及び屋根ふき材などの構造計算によって確認します.
一方,「二次設計」とは,大地震などによっても建築物が倒壊などをしないことの確認を行うことです.具体的は検討内容については,建築物の形状や規模によってルート2及びルート3のように異なります.
ルート1は,比較的小規模な建築物に対象を限定するとともに,鉄筋コンクリート及び鉄骨鉄筋コンクリート造については,一定以上の壁量や柱量を確保することにより,鉄骨造については,地震力の割り増しや筋かい及び接合部の破断防止を確認することにより耐震性を持たせようとするものです.
なお,ルート1については,一定以上の壁量などがあること(RC造及びSRC造),あるいは地震力の割り増し(S造)を行うことにより,大地震時の検討である二次設計は行わなくても良いということになっています.
鉄筋コンクリート造の二次設計について,少し詳しく見てみましょう.
数式の具体的な数値などを覚える必要はありません.
ルート1の式を満足する建築物は,多くの耐力壁及び柱により十分な耐力を持つため,大きな靭性は必要としない,強度型の建築物となります.このルート1の式を満足する建築物は大地震などの検討の二次設計は不要となります.
なお,AwやAcが何を意味しているのかについては過去問題で出題されていますので,確認しておく必要があります.
ルート1の式を満足する耐力壁や柱がない建築物については,層間変形角,剛性率・偏心率,塔状比のそれぞれの規定に満足する場合は,ルート2-1あるいはルート2-2のこれらの式を満足する場合はルート2-1あるいはルート2-2により二次設計の確認を行うことになります.
ルート2-1は,剛性や重量のかたよりが少なく,耐力が大きく,かつ,やや靭性のある建築物が対象となります.耐力壁が水平力の多くを負担する建築物となります.
ルート2-2は,剛性や重量のかたよりが少なく,耐力が大きく,かつ靭性のある建築物が対象となります.耐力壁とはみなされない壁やそで壁の付いた柱が水平力の多くを負担する建築物となります.
それぞれの式や規定を満足しない建物,及び規模の大きい建物はルート3である保有水平耐力の計算を行うことになります.
なお,平成27年1月の告示改正により,ルート2-3は廃止されました.
鉄骨鉄筋コンクリート造の二次設計については,基本的には,鉄筋コンクリート造と同様です.
ルート1やルート2のそれぞれの数式の数値が異なりますが,RC造とSRC造は同じような検討方法であるということを知っておけば対応可能です.
次に,鉄骨造の二次設計について,少し詳しく見てみましょう.
鉄骨造のルート1は,比較的小規模な建築物に対象を限定するとともに,地震力の割り増し(一般的な地震力の算定では,中地震についてはCoを0.2以上としているのに対し,地震力を1.5倍のCoを0.3以上とします)や,筋かい端部及び接合部の破断防止などを確認することにより耐震性を確保する耐震計算ルートです.RC造及びSRC造と同様,ルート1を満足するS造の建築物については大地震などの検討の二次設計は不要となります.
建築物の規模(階数、面積及び柱スパン)によって,ルート1-1と1-2の2種類があります.
ルート1-2の場合は,ルート1-1の検討に加えて,偏心率が15/100以下であることを確認する必要があります.
ルート2については,RC造やSRC造と同様,層間変形角、剛性率・偏心率,塔状比のそれぞれの規定を満足させる必要があります.
一次設計用の地震力については,靭性型か強度型かによってCoを0.2から0.3の間で割増します.
筋かいの水平率分担率βによって割増しを行います.


ルート1及びルート2の規模や規定が満足しない建築物についてはルート3である保有水平耐力の計算を行うことになります.
■学習のポイント
これらの最低限,覚えなければならない事項はありますが,まずは耐震計算フローを見ながら,過去問題を見ることで,どの辺が繰り返し出題されているのかを肌で感じて下さい.
06.鉄骨構造
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分30秒)
この項目は,問題数が非常に多く,覚えることも多いため,勉強するにも嫌気がさしてくる単元の一つではないでしょうか?
このように,広い範囲から出題される項目に関しては,余り一つの事柄に深く入り込むのではなく,まずは,広く浅く知識を広げていくのがポイントです.他の科目にも共通している点として,建築士試験では,一級建築士としては知っていていただきたい重要事項を出題されていることがあげられます.ですから,まずは,過去問題とその解説を一読することをオススメします.
座屈等に関して
梁の横座屈は,H形鋼などの開断面の梁が曲げを受けた時,圧縮側のフランジ等が面外に座屈し,ねじれを生じ,曲げ耐力が低下する現象を指します.梁の材軸と(通常は,柱ならば縦方向,梁ならば横方向)直交方向にフランジが変形しないようにすることで横座屈は防止できます.
横補剛とは,小梁などで梁フランジの面外変形を拘束し,横座屈を防止するために用いられます(問題コード26172).
柱や梁の端部,筋かいの端部や中央部のフランジやウェブなどが圧縮を受けると,それらが局所的に波打つように変形することがあります.これを局部座屈といいます.
H型鋼などの柱材方向に平行方向のスチフナ(鋼板)は,柱では縦スチフナ,梁では水平スチフナと呼ばれます.また,材軸と直交方向に入れるスチフナは,梁でも柱でも中間スチフナと呼びます.中間スチフナは,ウェブの局部座屈を防ぐのに力を発揮します(問題コード13171).
局部座屈は,フランジやウェブの幅厚比(フランジなどの幅/厚さ)と鋼材の降伏比に関係しています.フランジやウェブの幅厚比が小さいほど,鋼材の降伏比が小さいほど,局部座屈は生じにくく,部材の靭性は高くなります.
細長比に関して
柱の有効細長比は200以下(柱以外の場合には250以下)とします.
引張材は,高力ボルトの孔などによって断面欠損のある場合は,断面欠損を考慮した有効断面積で算定します.
山形鋼やみぞ形鋼などをガセットプレートの片側にのみ設ける場合には,偏心による曲げの影響を考慮して設計します.通常の場合,その突出脚の1/2の断面を無効とした断面で算定します(問題コード29152ほか).ボルトの数によって無効とする突出脚が変化しますが,それについてはこちらの資料(←別ファイルが開きます)が参考になると思います.
ボルト接合に関して
中ボルト接合と高力ボルト接合の2種類に分類できます.
中ボルトを用いたボルト接合では,下図に示すように中ボルトの軸部に作用するせん断力により応力が伝えられます.
力の伝達としては,鋼板1からボルト軸部へは支圧,ボルト軸部内部ではせん断,ボルト軸部から鋼板2へは支圧で伝わります.
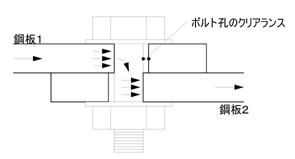
高力ボルト接合には,摩擦接合と引張接合の2種類があります. .
高力ボルト摩擦接合では,高力ボルトが鋼板を締め付ける圧縮力で鋼板の接触面に生じる摩擦力により応力が伝えられます.
しかし,接合部に作用する力を次第に大きくすると,摩擦が切れ,高力ボルトの軸部が鋼板のボルト孔の側面に接触することになります.この状態では,中ボルトのように,高力ボルトの軸部に作用するせん断により応力が伝えられます.
つまり,高力ボルト摩擦接合では,許容応力度設計では摩擦で応力が伝達され,破断耐力(終局耐力)の計算では,摩擦が切れた後の応力はボルト軸部のせん断で応力が伝えられます.(問題コード13172)
摩擦面における滑り係数は,鋼板の赤錆面では0.45,溶融亜鉛めっき面では0.4です.
保有耐力接合に関して
大地震時の安全性を確認する保有水平耐力計算や耐震計算ルート1の計算で用いる,崩壊メカニズム時の応力状態において柱及び梁の仕口部及び継手部や筋かい材の端部及び接合部が破断しない接合方法を保有耐力接合と呼びます.
溶接接合に関して
構造部材の溶接接合には,一般には,突合せ溶接やすみ肉溶接が用いられます.その溶接記号に関してもチェックしておきましょう(問題コード21171).
突合せ溶接の継目に作用する応力は「引張,圧縮,せん断」であり,すみ肉溶接の継目には「せん断」が作用します(問題コード23173).溶接の継目の短期許容応力度と材料強度は同じ値と定められています.長期許容応力度はこれらの数値の1/1.5の値です.
溶接の有効面積は,「溶接の有効長さ」×「有効のど厚」により求められます.板厚が異なる時は,薄い方の板厚が有効のど厚になります.
すみ肉溶接は「すみ肉サイズの10倍以上,かつ40mm以上の長さのもの」を有効とし,その有効長さは「溶接の全長からすみ肉サイズの2倍を引いたもの」と定められています(問題コード21171).すみ肉ののど厚は「すみ肉サイズの1/√2倍」になります.
突合せ溶接とすみ肉溶接のせん断許容応力度は同じ値となりますが,圧縮・引張・曲げに関しては突合せ溶接はすみ肉溶接の√3倍の値となります(問題コード19153).
ボルトおよび高力ボルトと溶接との併用に関して
一つの継手の中に高力ボルトと溶接とを併用する場合,先に溶接を行うと溶接熱によって板が曲がり,高力ボルトを締め付けても接合面が密着しないことがあるので,両方の耐力を加算することができないが,先に高力ボルトを締め付けた場合には溶接による板の変形は拘束されるので,両方の許容力を加算してもよい(問題コード30173ほか).
継手にリベットを使用した建築物を増築または改築する場合は,既存時の使用中の応力によって,起こりえたかもしれないリベットのすべりは,すでに起こってしまっていると考えられるので,これらのリベットはそのまま既存建物の固定荷重を負担し,増改築分の固定過重および積載荷重による応力を溶接によって伝えるよう継手を設計してもよい(問題コード18182).
高力ボルトを用いた既存建物を増改築する場合も,同様の方法で溶接との併用継手を設計してよい.
柱脚について
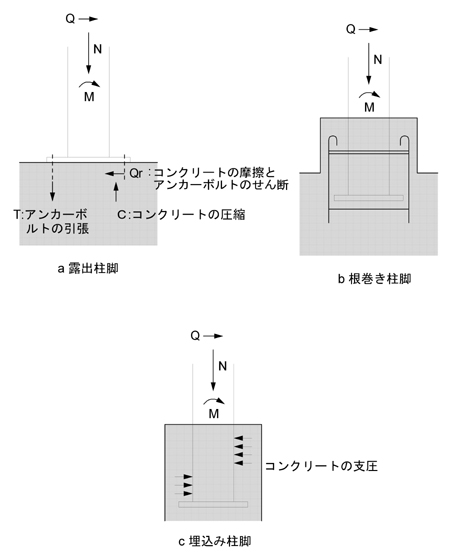
「露出柱脚,根巻き柱脚,埋込み柱脚」の3つの特徴を覚えましょう.
「露出柱脚」とは,アンカーボルトとベースプレートにより鉄筋コンクリート構造と鉄骨柱が接合されたもので,軸力と曲げモーメントはベースプレートとアンカーボルトを介して基礎に伝達されます.せん断力はベースプレート下面とモルタルまたはコンクリートとの摩擦力,またはアンカーボルトの抵抗力により伝達されます(問題コード18184).
軸部の降伏に先立ってねじ部で破断が生じないような,軸部の塑性化が十分に保証された「転造ねじアンカーボルト」に関する出題もあります(問題コード29161).
「根巻き柱脚」とは,下部構造から立ち上げられた鉄筋コンクリート柱に鉄骨柱が包み込まれた形状で,圧縮軸力は根巻き部分の鋼柱およびベースプレート,引張軸力は根巻き部分の鋼柱およびアンカーボルトを介して基礎に伝達されます.曲げモーメントとせん断力は根巻き鉄筋コンクリート部分で伝達されます.
根巻き鉄筋コンクリートの高さは,柱せいの2.5倍以上とします(問題コード29163).
「埋込み柱脚」とは,下部の鉄筋コンクリート構造に鉄骨柱が埋め込まれた形状で,軸力は鉄骨柱脚部のベースプレートを介して基礎コンクリートに伝達されます.曲げモーメントとせん断力は基礎コンクリートと鉄骨柱の埋め込み部との間の支圧により伝達されます.
基礎コンクリートへの鉄骨柱の埋め込み深さは,柱せいの2倍以上とします(問題コード28164).
■学習のポイント
ここ数年,新しい項目に関する出題が増えてきています.
しかし,ほとんどの新問が正答肢(その問題が○や×となる決め手の選択肢)とはなっていないので,そんなに心配する必要はないと考えます.
まずは,毎年繰り返し出題されている過去問題を制覇しましょう!
07.鉄筋コンクリート構造
まずは,オンライン講義の様子をご覧ください(Youtube動画 約6分)
施工科目の「鉄筋工事」や「コンクリート工事」は,鉄筋加工における注意点や型枠の存置期間など施工工事から見た出題ですが,この項目では鉄筋コンクリート部材を設計手法から見た事柄に関して出題されています.
鉄筋コンクリートというのは,引張に弱いコンクリートを鉄筋で補強している理にかなったものです.コンクリートがアルカリ性であるため,錆に弱い鉄筋を保護している意味合いもあります.また,コンクリートと鉄の熱膨張率(線膨張係数)がほぼ等しいため,温度の変化における悪さもありません.
鉄筋コンクリート構造の場合は,柱や梁がせん断破壊を起こさないで曲げ破壊をさせる,耐震壁がせん断破壊をおこさないで曲げ破壊や基礎の浮き上がりが生じるようにさせることがポイントです.
そのために,柱や梁などについていろいろな規定があります.
そのことを踏まえて,過去問題とその解説を一読してみてください.
柱や梁をせん断破壊させないことが前提としてありますので,せん断補強筋(帯筋やあばら筋)によってせん断力に抵抗します.そのために,せん断補強筋比の規定があります.
また,鉄筋コンクリート部材では,せん断力に対して,コンクリートのせん断強度とせん断補強筋の効果を組み合わせて設計します.しかし,柱の長期許容せん断力に関しては,せん断ひび割れを許さないとして,コンクリートの許容せん断応力度のみを有効としています.これは鉄骨鉄筋コンクリート柱の場合と同様です(問題コード14131・・・鉄骨鉄筋コンクリート).
コンクリートのヤング係数はコンクリート強度が高くなるほど大きくなります(「コンクリート」のインプットのコツ参照)が,鉄のヤング係数は強度によらずほぼ一定である(「鋼材・金属」のインプットのコツ参照)ため,コンクリートに対する鉄筋のヤング係数比(鉄筋のヤング係数/コンクリートのヤング係数)は,コンクリート強度が高くなるほど小さくなりますが,構造計算では,通常のコンクリート強度ではヤング係数比を15と仮定します.
一般に,鉄筋コンクリートの曲げ材は,コンクリートの圧縮側が破壊するより先に引張側の鉄筋(主筋)が降伏するように設計します.このことを「引張鉄筋比が釣り合い鉄筋比以下の場合」と言いますが,この時の許容曲げモーメントはM=at×ft×j=7/8×at×ft×d(ここで,at:引張鉄筋の断面積,ft:鉄筋の許容引張応力度,j:曲げ材の応力中心距離(=7/8d),d:曲げ材の圧縮縁から引張鉄筋重心までの距離(有効せい)を指します)で,終局曲げモーメントはM=0.9×at×σy×dで計算できます(問題コード問題コード23111ほか).
かぶり厚さとは,鉄筋表面とこれを覆うコンクリート表面までの距離を指し,鉄筋の耐火被覆やコンクリートの中性化速度などを考慮して定められています(問題コード27123).
ここで,よく質問が来る鉄筋コンクリートの接合部での力の伝達方法(問題コード01142)について説明します.
鉄筋コンクリート構造ラーメン構造の柱梁接合部の設計法としては
・水平荷重(特に地震荷重)に対する短期設計を対象としています.
・長期荷重時のせん断力は小さく,接合部のひび割れが問題となった事例もほとんどないため,長期荷重に対しては通常は考えません.
・水平荷重を受けるラーメン内の柱梁接合部は,下のような応力状態となります.

・梁主筋は,一般に,釣り合い鉄筋比以下で配筋されていますので
→引張側の鉄筋降伏で梁の曲げ耐力が決まります.
→引張鉄筋量を増やしても,釣り合い鉄筋比であれば,引張側の鉄筋降伏で梁の曲げ耐力が決まります.
→引張鉄筋量が増えると,上図におけるTが大きくなります.
→(梁の)Tが大きくなると,(梁の)Cs+Ccも大きくなります.
→その結果,柱梁接合部に生じるせん断力Qjも大きくなります.
また,鉄骨造柱と同様,鉄筋コンクリート柱も大きな軸力を受ける柱ほど地震時の粘り強さが減少することに注意して下さい.
梁部材における鉄筋とコンクリートとの許容付着応力度は,上端筋よりも下端筋の場合の方が大きいことに注意しましょう.
梁などのクリープ現象を制御するためには,圧縮鉄筋が有効となります.圧縮力を受ける柱では,コンクリートがクリープによって縮もうとする分,鉄筋の圧縮力の分担が増えるため,鉄筋の圧縮応力は徐々に増加します(問題コード01124ほか).
ひび割れに関しては,図問題として出題されています(問題コード25141,29111).鉄筋コンクリート構造(部材)に入る基本的なひび割れについて整理しておきましょう.
鉄筋コンクリート造の部材設計に関しては,計算外規定(注意点)があります.
簡単にまとめてみますと
・柱
・主筋比は,0.8%以上とします.
・帯筋比は,0.2%以上とします.
・梁
・長期荷重時に正負最大曲げモーメントを受ける部分の引張鉄筋比は0.4%以上,
または存在応力によって必要とされる量の4/3以上とします.
・主要な梁は,全スパンにわたり複筋ばりとします.
・あばら筋比は,0.2%以上とします.
・あばら筋の間隔は,3/4D(D:梁せい)以下とします.
・柱梁接合部
・柱梁接合部内の帯筋も帯筋比を0.2%以上とします.
・帯筋間隔は150mm以下,かつ隣接する柱の帯筋間隔の1.5倍以下とします.
・床スラブ
・最大曲げモーメントを受ける部分における引張鉄筋間隔は,短辺方向には20cm以下,
長辺方向には30cm以下,かつ床スラブの厚さの3倍以下とします.
・全断面の鉄筋比は0.2%以上とします.
・耐震壁
・耐力壁の厚さは12cm以上とします.
・壁筋は径9mm以上で,配筋間隔は縦横に30cm以下とします.
・耐震壁周囲の付帯ラーメン
・梁の全断面に対する主筋の鉄筋比は0.8%以上とします.
■学習のポイント
鉄筋コンクリート構造は,毎年4問程度出題されている頻出項目です.収録されている問題数も非常に多いですが,繰り返し出題されている問題から優先的に勉強しましょう♪
08.鉄骨鉄筋コンクリート構造
まずは,オンライン講義の様子をご覧ください(Youtube動画 約6分30秒)
鉄骨鉄筋コンクリート構造を苦手にしている人はかなり多いと思います.鉄筋コンクリート構造などに比べて,部材設計などが難しいからです.
特徴的なものとして,累加強度の考え方があります.単純累加強度とは,鉄骨の強度と鉄筋コンクリートの強度をそれぞれ求め,それらを加える方法です.それぞれの強度を単純に加える(累加する)ので,単純累加強度,略して累加強度と言います.鉄骨鉄筋コンクリートの曲げに対する設計に用います.
似たような言葉に一般化累加強度というものがあります.これは,柱のような曲げと軸力を受ける部材の耐力を求める際に,鉄骨と鉄筋コンクリートそれぞれの曲げと軸力を組み合わせた耐力を最大になるように加える(累加する)方法です.保有耐力の算定などに用います.
この考えが,鉄骨造や鉄筋コンクリート造とは異なる部分ですので,難しいと思われると思います(問題コード22194).
そのことを踏まえて,過去問題とその解説を一読してみてください.
梁のせん断に対して許容応力度設計を行う際には,鉄骨部分と鉄筋コンクリート部分のそれぞれのせん断力を求めて,鉄骨部分と鉄筋コンクリート部分のそれぞれの許容せん断力以下となるようにします.
ここで,それぞれのせん断力とは,鉄骨部分と鉄筋コンクリート部分の設計用曲げモーメントより求めます(問題コード23192).
上記説明における累加強度ではないことに注意しましょう.
また,鉄筋コンクリート部分の許容せん断力は,せん断補強筋比の上限は0.6%とします.
梁のせん断に対して保有耐力計算を行う際には,鉄骨部分と鉄筋コンクリート部分のそれぞれの終局せん断耐力の累加とします(問題コード24192).上記説明における累加強度を用いるわけです.
柱の長期許容応力度設計では,ひび割れを生じさせないように(この考え方は鉄筋コンクリート造の場合と同様です),鉄骨の補強効果を考慮した鉄筋コンクリートのひび割れ強度以下になるようにします(問題コード14131).
柱のせん断に対して許容応力度設計を行う際には,鉄骨部分と鉄筋コンクリート部分のそれぞれのせん断力を求めて,鉄骨部分と鉄筋コンクリート部分のそれぞれの許容せん断力以下となるようします(問題コード27231).累加強度ではないことに注意しましょう.
柱のせん断に対して保有耐力計算を行う際には,鉄骨部分と鉄筋コンクリート部分のそれぞれの終局せん断耐力の累加とします(問題コード01234).上記説明における累加強度を用いるわけです.
柱の設計において,鉄骨量が多いとコンクリートの充填性が悪くなるため,鉄骨量に応じてコンクリート強度を低減して考えます(問題コード22193).
柱梁接合部のせん断に対して許容応力度設計を行う際には,鉄骨部分と鉄筋コンクリート部分のそれぞれの許容せん断力の累加とします.
上記説明における累加強度を用いるわけです.
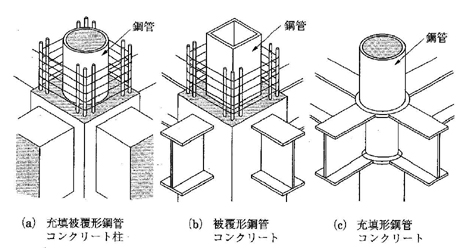
せん断補強筋量としては,内蔵鉄骨がH型鋼のような開断面充腹形鉄骨の場合は,内蔵鉄骨のウェブが部材(柱や梁)のせん断力に効果的に効くため,通常の鉄筋コンクリートのせん断補強筋比の半分程度ということで,あばら筋比,帯筋比はともに0.1%以上とします.内蔵鉄骨がラチス形や格子形のようにウェブが鋼板で満たされていない(空間がある)ような非充腹形鉄骨の場合は,内蔵鉄骨のウェブが部材(柱や梁)のせん断力に効果的に効くとは思えないため,鉄筋コンクリート同様にあばら筋比,帯筋比はともに0.2%以上とします.下図のような被覆形及び充填被覆形鋼管コンクリート構造の場合のあばら筋比や帯筋比は0.2%以上となっていますが,これはあばら筋比や帯筋比の求め方が開断面充腹形や非充腹形の場合と異なるためです.
開断面充腹形の0.1%と被覆形の0.2%の実際のせん断補強筋量は同じくらいと考えてもいいと思います(問題コード20145ほか).
また,鉄筋コンクリート部分の許容せん断力の算定では,せん断補強筋比の上限は0.6%とします.
柱における鉄骨と鉄筋の断面積の和は,コンクリート断面積の0.8%以上必要であることに注意しましょう(問題コード20155ほか).
鉄骨のかぶり厚さは最小5cm,通常は10cm以上とします.
施工時の検討(建て方検討)に関しても注意が必要です.
通常,鉄骨鉄筋コンクリート造は,鉄骨の建て方を行い,鉄筋の配筋を行い,コンクリートの打設を行う順序で施工されていきます.コンクリートの強度が出現した後に関しては累加強度が成り立ちますが,コンクリート強度が出現する前では,鉄骨造の場合と同様と考えられます.通常の鉄骨造の鉄骨と鉄骨鉄筋コンクリート造の内蔵鉄骨では,鉄骨鉄筋コンクリート造の内蔵鉄骨の方が部材が小さいことが一般的であるため,コンクリート強度が出現する前での風や地震に対する安全性の検討が必要になります(問題コード13153ほか).
■学習のポイント
コンクリート充填管(CFT)部材に関する出題が増えています(問題コード30264ほか).これらの問題・解説について理解しておきましょう.
また,部材の終局せん断耐力算定に関しては,問題コード01234では,「累加する鉄骨と鉄筋コンクリートのそれぞれの終局せん断耐力は,曲げで決まる場合とせん断で決まる場合の小さい方とする」というように更に突っ込んだ問題となっています.このことに関しても覚えておきましょう.
鉄骨鉄筋コンクリートに関しては,過去に繰り返し(複数回)出題している問題を理解しておけば,十分対応できると考えられます.
11.地盤・土質
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分30秒)
この地盤・土質項目を苦手にしている人も多いと思います.
すごく大きく見てみると,建築物は地盤に支えられていますよね.地盤が悪いところでは杭で建築物を支持する杭基礎形式で,地盤が比較的良いところでは直接基礎形式です.こられ基礎に求められている性能(要求性能)は,建築物が沈んだり傾いたりしないことですよね.
つまり,地盤・土質項目での重要ポイントは,「地盤の支持力」と「地盤の沈下量」と言えます.
地盤の性質として,覚えておくこととして,土の構成があります.土は,土粒子と水と空気からなっています.土粒子の大小関係は,粘土<シルト<砂となります(問題コード23231ほか).
地質の地盤区分として,洪積層(良質地盤,年代が古い)と沖積層(軟弱地盤,年代が新しい)とがあり,地盤の堅さとしては,沖積層<洪積層となります(問題コード24213).
圧密沈下とは,主に粘性土地盤で生じ,土に圧力が長時間継続的に加わる場合,土中の間隙水が徐々に搾り出され,間隙が減少し,地盤が沈下することを示します.
粘性土は透水性が小さいため,水の移動に時間がかかり,圧密沈下は一般的には時間がかかります.また,現在の有効上載圧力(現在加わっている圧力)より過去に受けた上載圧力が大きい地盤は過圧密の状態にあると言います.
現在の有効上載圧力より更に荷重を加えても,圧密先行荷重(過去に受けた最大の上載圧力)に達するまでは圧密沈下は生じません.圧密が進んでいる状態の地盤は,圧密未了状態にあると言います.
即時沈下とは,主に砂質地盤で生じ,早期に沈下を起こし,安定します.沈下量は小さいです(問題コード01211ほか).
砂質地盤の液状化について簡単に説明します.
液状化とは,振動によって土中の間隙水圧が高くなり,土粒子間に働く有効応力がゼロになる現象を指します.この表現は,実際に過去に出題された問題そのものです.間隙水圧?有効応力?難しい言葉がでてきますね.
有効応力(土粒子間に生じる応力)などに関して深く学ぶ必要はありません.液状化に関しては,以下に示す液状化現象が起こりやすい4要素を覚えておきましょう.
1.飽和地盤で細粒土含有率が低い(細粒土含有率が低いとは,土粒子の小さい粘土成分が少ないこと,つまり土粒子の大きい砂成分が多いことを指します).
2.飽和地盤のN値が小さい.
3.地下水位面が地表面に近い.
4.地震入力が大きい.
下図の横軸は地盤のせん断ひずみ(地盤の変形量)で,左側のせん断ひずみは小さく(小さい地震動時の地盤の変形),右側に行くほどせん断ひずみは大きく(大きい地震動時の地盤の変形)なります.縦軸のG/G0とは,地盤のせん断剛性低下率で,ある時点での地盤のせん断剛性が,地盤が元々持っているせん断剛性からどれくらい低下したのかを示します.つまり,地盤の剛性(堅さ)の低下率を指します.図からわかるように,剛性低下率(G/G0)は右下がりの曲線ですので,地盤内に発生するせん断ひずみが増加するほど(大きな地震で地盤が揺れるほど),地盤のせん断剛性は低下することがわかります.
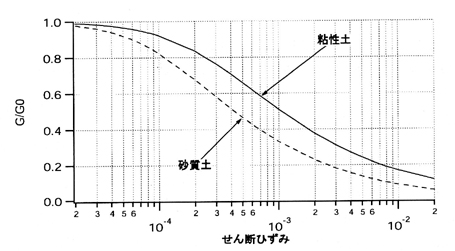
一方,地盤の減衰定数は,右上がりの曲線ですので,盤内に発生するせん断ひずみが増加するほど(大きな地震で地盤が揺れるほど),地盤の減衰定数は増加することがわかります.
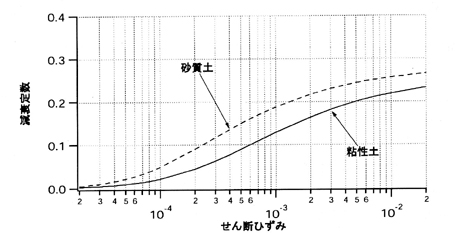
この地盤の減衰特性は,上部建物と性状が異なりますので,上部建物とは完全に切り分けて理解して下さい.
これら2つの事象については,上記のグラフをイメージできるようになりましょう!
続いて,地盤調査に関して説明します.
地盤調査とは,原位置試験と土質試験に分けられます.
原位置試験とは,地盤内の土の性質を直接調べる試験のことで,
標準貫入試験(問題コード20194)
平板載荷試験(問題コード29192)
スウェーデン式サウンディング試験(問題コード24223)
ボーリング孔内水平載荷試験(問題コード01204)
ベーン試験,常時微動測定(問題コード29193)
せん断波速度測定(PS検層)(問題コード28214)
などがあります.
土質試験とは,ボーリングなどによってサンプリングされた試料を用いて行う物理的,化学的,力学的性質を調べる試験のことで,
粒度試験(問題コード27192) や密度試験などのような物理的試験(砂質土,粘性土などの土質判別を行う試験)と,1軸圧縮試験,3軸圧縮試験(問題コード25231ほか),圧密試験(問題コード26224)や透水試験などの力学的試験(土の強さ,圧縮性,動的性質などを調べる試験)があります.
最後に地盤改良と液状化対策,圧密沈下対策に関して説明します.
地盤改良について
1.締固め工法(バイブロフロテーション工法,サンドコンパクションパイル工法など):砂質土に振動や衝撃力を加えて安定した地盤を造る工法
2.間隙水圧消散工法(グラベルドレーン工法など):砂質土地盤中に透水性のよい粗骨材の柱を作り,地震により発生した間隙水圧を短時間で消し去る工法
3.強制圧密脱水工法(サンドドレーン工法など):軟弱な粘性土を強制的に圧密し,事前に沈下させ強度を増加させる工法
4.脱水工法(生石灰杭工法など):軟弱な粘性土地盤中の間隙水を,脱水材や発熱する材を用いて脱水し,強度の増加を図る工法
5.固結工法(深層混合処理工法など):セメントなどを注入し,地盤の不透水化や強度の増加を図る工法
6.置換工法:軟弱地盤を良質の地盤に置き換える工法
液状化対策としては,締固め工法(バイブロフロテーション工法,サンドコンパクションパイル工法など)が,圧密沈下対策としては,間隙水圧消散工法(グラベルドレーン工法など)が有効とされています.
なお,各工法の詳細に関しては,上記○○工法などで検索してみてください.
■出題のポイント
問題コード01191ほかの問題文と上で述べた液状化現象が起こりやすい4要素に関する質問が多いので,補足説明します.
まず,細粒分含有率と細粒土含有率は同じものと思ってください.細粒分含有率(細粒土含有率)が大ということは,砂より粘土が多いことになります.
続いて含水比に関して
まず「ある領域内」にある土を考えます(「だるま落とし3段重ね」をその領域と考えて下さい).土というのは,だるまの一番下の段にあたる「土粒子」と,真ん中の段にあたる「水」と,一番上の段にあたる「空気」から成り立っています.土の含水比とはそのうちの「土粒子の重量Ws」で「水の重量Ww」を割った,Ww/Wsを百分率で表したものです.ここで,含水比は重量比であり体積比ではないことに注意して下さい.
そして,ある領域内における土の大きさ(つまりだるまの1段目の大きさ)が同じならば,水の重量(2段目の大きさ)が大きい程含水比も大きいと言うことになります.
さらに,細粒分含有率(細粒土含有率)が高くなるとなぜ含水比が大きくなるかという説明に行きます.土粒子というのは,水分中にあると周辺の水分子と電気的に吸着する性質があります.粒径が細かいと表面積が広くなるため,その分多くの水を引きつけます.そのため,同じ体積の砂と粘土では引きつけられる水の量が違ってくるのです.粘土の方が粒径が細かい為,より多くの水を引きつけるので,含水比も大きくなります.
これらのことと,上で述べた液状化現象が起こりやすい4要素より,土の含水比は細粒分含有率が大きくなるほど大きくなるのに対し,液状化は細粒土含有率が少ないとおきやすいということがわかると思います.過去問20年分の「知識」で,地盤・土質に関するほとんど全ての性質が網羅されています.
施工科目に収録されている地盤の解説集も参考にしてください.
12.基礎構造
まずは,オンライン講義の様子をご覧ください(Youtube動画 約5分)
まず最初に地盤の許容応力度に関する説明から始めます.
地盤の地耐力とは,極限支持力以内で,更に沈下量が上部構造に有害な影響を与えることのない限界沈下量以下となるような荷重(応力度)を指します.
簡単に言うと,「地盤の許容応力度」と「沈下量が許容沈下量となるときの応力度」のうちの小さい方というわけです.
基準法令第93条に基づく告示(平成13年国交告第1113号第二項)より,地盤の許容応力度は,地盤調査に基づく場合と平板載荷試験に基づく場合,スウェーデン式サウンディング試験に基づく場合の3種類があることがわかります.
地盤調査に基づく地盤の長期許容応力度は
qa=1/3(icαCNc+iγβγ1BNγ+iqγ2DfNq)となっています.
icやαなどに関しても説明も記載されていますが,チンプンカンプンの式ですよね.
この式を分かりやすく言うと,( )内の
「icαCNc」は粘性土地盤の項,
「iγβγ1BNγ」は砂質土地盤の項,
「iqγ2DfNq」は根入れの項
による支持力です.
また,「 」内は「基礎の形状」×「支持地盤の強度」=「極限応力度」を意味しています.
また,地盤の短期許容応力度は
qa=2/3(icαCNc+iγβγ1BNγ+iqγ2DfNq)となっています.
つまり,地盤の許容応力度として,極限支持力度の1/3を長期許容応力度,2/3を短期許容応力度としています.これより,長期許容支持力度の極限支持力度に対する安全率は3であることがわかります.
かつ,短期許容応力度は,長期許容応力度の2倍であることがわかります.
また,平板載荷試験に基づく地盤の長期許容応力度は
qa=qt+1/3N’γ2Dfとなっています.1項目(qt)は平板載荷試験による降伏荷重度の1/2または極限応力度の1/3のうちいずれか小さい方,2項目(1/3N’γ2Df)は根入れの項となっています.
短期許容応力度は
qa=2qt+1/3N’γ2Dfとなっています.
これらを見比べてみると,根入れの項の数値が同じため,平板載荷試験に基づいて地盤の許容応力度に関して,「根入れの効果を考慮した場合の短期許容応力度は,長期許容応力度の2倍とならない」および「根入れの効果を無視した場合の短期許容応力度は,長期許容応力度の2倍となる」ということがわかります(問題コード13192).
なおこれらの根入れの項による支持力とは,根入れ深さの部分の土が支持地盤の破壊を上から押さえて防止する効果のことを指しています.
また,基準法令第93条に記載されている地盤の許容応力度の表に目を通しておいてください.
基礎を設計する際に出てくる言葉に関して,少し説明します.
使用限界状態とは,想定する荷重を日常的に作用する荷重を,
損傷限界状態とは,1回から数回遭遇する荷重(50年に1度程度)を,
終局限界状態とは,500年に1回程度の最大級の荷重を
想定しています.
それぞれの限界状態に対しての検討を行います.
杭の鉛直支持力は,載荷試験によって求めることが望ましいですが,載荷試験を行わない場合は,工法に応じた支持力計算式から求めます.
告示(平成13年国交告第1113号第五項)では,打込みぐい,セメントミルク工法による埋込みぐい,およびアースドリル工法等による場所打ちぐいの先端の地盤の許容応力度(qp)を以下のように示しています.
打込みぐい :qp=300/3×N
埋込みぐい :qp=200/3×N
場所打ちぐい:qp=150/3×N
つまり,先端支持力は,場所打ちぐい<埋込みぐい<打込みぐいの順になっています(問題コード22232).
基礎の設計に関して,よく質問が来る問題として問題コード15185があります.基礎構造に対する構造算定をする際に基礎部分の重量を「含む」のか「含まない」のかに関することです.
これには2つのポイントがあります.一つは,基礎スラブの底面積の算定(底面積の大きさを決めることです)で,もう一つは,基礎スラブの断面算定(フーチングに生じる曲げモーメントやせん断力によりフーチングのコンクリート強度や高さなどの大きさを決めることです.曲げモーメントによりフーチングの配筋を決め,せん断力によりコンクリート強度を決めることが多いです)です.
まず一つ目の底面積の算定の場合は,「(フーチングにつながっている)柱からくる軸力(これは上部建物の荷重のことですね)+フーチングなどの基礎自体の重量+基礎部分の上にある埋め戻しの土の重量」の合計でフーチングが地面にめり込まないように底面積を求めます.「柱からくる軸力+基礎自体の重量+埋め戻し土の重量」をフーチング底面積で割った値が地耐力より小さければフーチングがめり込むことはありません.
続いて,その二の基礎の断面算定(つまり基礎の強度などを求めることに関してですが)でのポイントは,その一でフーチングが地面の中にめり込まないような大きさを持っているので,フーチングの重量(下向き)は,接地圧(フーチングが地面から上向きに受ける力)で打ち消しあい,フーチングに応力を生じさせないっていうことです.それと,フーチング上の埋め戻し土量は軽微な場合が多いので通常は無視するということです.その結果として,フーチング重量や埋め戻し土の重量を含まない上部建物からくる柱荷重のみがフーチングに応力を発生させることになります.よって,この柱軸力によって生じる応力が持つように配筋やコンクリート強度などを決めるわけです.
また,問題コード29214の負の摩擦力に関する質問も多く来ます.負の摩擦力とは,ある地層が圧密などにより沈下する際に,杭に下向きの軸力を生じさせてしまうことを言います.杭の設計時に,その地盤沈下による軸力(下向き)を考慮していない場合には危険側になるので,注意しなければなりません.支持杭と摩擦杭で,負の摩擦力の影響は,支持杭の方が多く受けます.これは,負の摩擦力とは,杭の沈下量と地層の沈下量との相対差によって生じるわけですがら,摩擦杭のように,地層と杭とか同じような沈下をする場合には,相対差は小さくなるため,負の摩擦力の影響は小さくなると言えます.
土圧に関しては,施工の土工事・山留め工事の項目で説明します.
■出題のポイント
過去問20年分の「知識」で対応できる問題については,頑張って理解しましょう.
13.その他(免震構造・制振構造)
まずは,オンライン講義の様子をご覧ください(Youtube動画 約4分)
今回のインプットのコツでは,免震・制振に関して,概要説明します.
ここ数年は,かなり専門的な内容の出題もありますが,まずは全体把握を心がけましょう!
免震構造は,建築物の基礎部分あるいは中間部分に「免震層」をつくることで,建築物を地面と絶縁することで,地震動の揺れを建築物に極力伝えないような構造です.
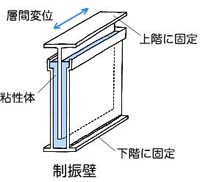
一方,制振構造は,建築物の中にあらかじめ仕込んだ制振部材で地震力を消費させ,柱や梁が壊れないようにする構造です.
制振構造には,建築物に仕込まれたダンパーで地震力を消費されるパッシブ制振と,電子制御で建築物の揺れを減らすアクティブ制振があります.
免震建築物は,免震層の位置により基礎免震と中間層免震に分類されます.
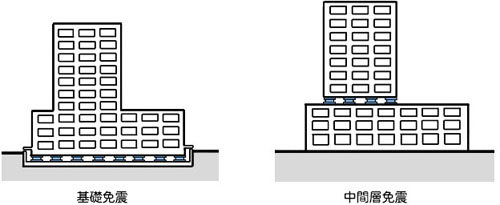
免震部材には,「絶縁機能」「復元機能」「減衰機能」「支持機能」の4つの機能が求められます.
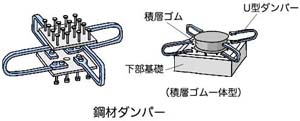
免震構造の免震層には,主に積層ゴムアイソレータが用いられます.
「絶縁機能」「復元機能」及び「支持機能」を持つ「天然ゴム系積層ゴムアイソレータ」の他に,「減衰機能」も持たせた「高減衰積層ゴムアイソレータ」や「鉛プラグ入り積層ゴムアイソレータ」も使われます.
「天然ゴム系積層ゴムアイソレータ」は「減衰機能」がないため,鋼材ダンパーやオイルダンパー等と組合わせて用いられます.
「天然ゴム系積層ゴムアイソレータ」は大きな引張力が生じる部分には使えません.
大きな引張力が生じる部分にはリニアスライダー等を用います.
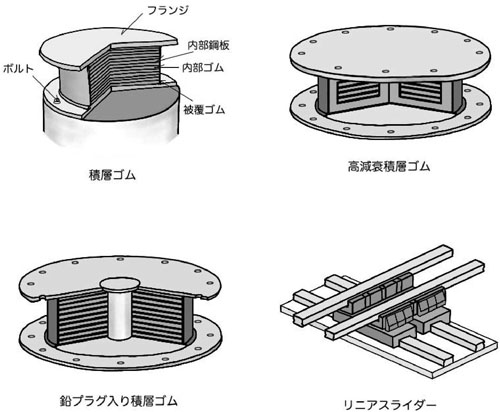
積層ゴムのゴム1層の厚さを小さくすると,鉛直支持能力を向上させることができます.
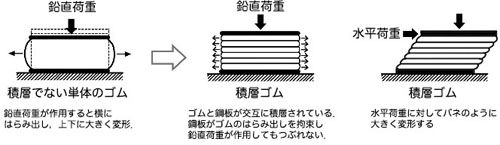
積層ゴムアイソレータ以外の支承には,すべり支承があります.
剛すべり支承と,剛すべり支承に積層ゴム部分が組み合わされた弾性すべり支承があります.
一般的なすべり支承には「絶縁機能」「減衰機能」「支持機能」の3つの機能は有してしますが,「復元機能」は有していません.
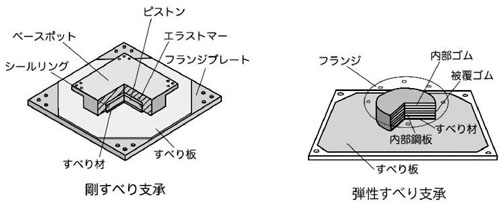
免震構造は,免震層より上部構造に伝わる地震動を,4~4.5秒の固有周期となるように長周期化することで,上部構造に生じる応答加速度が著しく低減する構造です.
制振構造とは,地震や風等による建築物の揺れを制御するような特性が付与された構造を指します.
制振構造は,強風時に塔状建築物が大きく揺れるような場合の居住性の改善や,地震による損傷,崩壊を防いで安全性を確保することを目的としています.
制振構造は,大きく分けて,パッシブ制振,アクティブ制振,ハイブリッド制振(パッシブ制振とアクティブ制振の組み合わせ)に分類されます.
パッシブ(受動的)制振とは,外部から力を加えて建築物の振動を制御することなく減衰特性を持たせることで振動を制御する形式をさします.
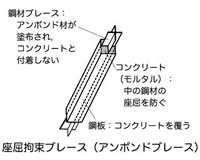
用いるダンパーには鋼材ダンパー等の「履歴減衰型ダンパー」や,「座屈防止ブレース」等があります.
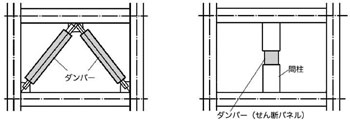
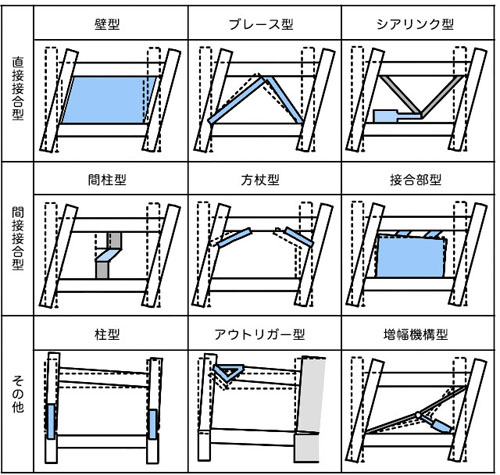
柱や梁よりも低強度のエネルギー吸収部材を設置するせん断パネル型のダンパーは,上下の主架構に制振部材を直結するタイプのブレース形式と,間柱の中間に設置するタイプの間柱形式とがあります.エネルギー吸収効率は,間柱形式よりもブレース形式の方が高くなります.
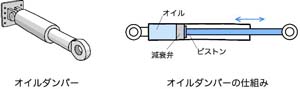
他にはオイルダンパーや粘性ダンパーのような「粘性減衰型(速度依存型)ダンパー」もあります.
□学習のポイント
最近出題が増えている免震構造,制振構造については,非常に専門的な内容が含まれているので,全てを理解することは不可能です.
あまり深入りせずに,過去問題の知識で4選択枝をジャッジできるように基本を押さえることがポイントです.
00.力学計算
力学計算全般について
合格ロケットでは,微分・積分の概念を使わず,足し算・引き算・掛け算・割り算の概念のみで「構造(力学計算編)」を説明してあります.これは,微分・積分アレルギーの人が多いからです.
微分・積分を用いないで力学計算を行おうとすると,式を暗記しなければどうしようもできなくなる部分があります.
これらの理由のため,計算式で導き出すのではなく,式を暗記して使いこなした方が得策であると判断した部分に関しては,インプットのコツ内で「○○を理解しましょう」という表現の他に,「○○を暗記しましょう」という表現を使っていきます.
まずは,「力学計算」の目次を見てみましょう.
01「静定・不静定」から10「固有周期」の問題まであります.(融合問題の11「その他」は除く.)
問題だけ,ぱらぱらっと目を通してください.
この中で,01「静定・不静定」と08「たわみ」の問題は,いくらでも難しい問題を作成することができます.
言葉を変えれば,02「断面の性質」,03「応力度」,04「全塑性モーメント」,05「崩壊荷重」,06「トラス」,07「座屈」,09「層間変位」,10「固有周期」の問題は,得点源になりえる単元なのです.
通常のテキスト・問題集は(合格ロケットも含めて),「静定・不静定」が単元の最初にあるため,勉強を始める際にテキスト・問題集の1ページ目から始めると,「静定・不静定」やその単元の基になる「力の釣り合い」,「力の流れ」や「N図,Q図,M図の描き方」の部分で『力学計算』が嫌になるケースが多く見られます.
そこで,インプットのコツとして,01「静定・不静定」はサラッと流して,02「断面の性質」から本格的に攻めていき,最後に,08「たわみ」の問題を勉強することをおススメします.
■学習のポイント
計算問題を学習するにあたっての超重要ポイント!
①問題文を読んで,何を求めれば良いのか(ゴールは何か)?を理解します.
②そのゴールに辿り着くためには,何を求めれば良いのか?を考えます.
③上記の②のゴールに辿り着くためには,何を求めれば良いのか?を考ます.
④上記の③のゴールに辿り着くためには,何を求めれば良いのか?を考ます.
⑤上記の③,④を繰り返します.
それにより,問題を解くに当たり,まず何からやれば良いのかの判断ができるようになります.
つねに,上記のことに意識を置くようにしてください!
01.静定・不静定
この部分は,構造科目を苦手にしている人にとっては,非常にとっつきにくい部分です.全てを完璧に理解しようとすると非常に多くの時間も労力もかかりますので,まずは,一通り広く,浅く勉強していきましょう.
では「静定・不静定」の問題を解く前に,合格ロケットに収録されている00基礎知識の解説を一読してみましょう.特に,00-2「力」の解説①~00-6「力の流れ」の解説(補足編)の部分は力学計算全体に関して基本となる部分です.
00-7「N図,Q図,M図」の解説,00-8「M図,Q図のイメージ」の解説で,N図,Q図,M図の基本となる部分を説明してあります.
■学習のポイント
ポイント1.「「外力系の力の釣り合い」→「内力系の力の釣り合い」で攻める!」
「N図,Q図,M図」を描く場合やトラスの問題などで共通している考え方として,『「外力系の力の釣り合い」→「内力系の力の釣り合い」を考える』ということがあります.
具体的には,「外力系の力の釣り合い」を考えて,外力によって生じる『支点反力』を計算します.次に,「内力系の力の釣り合い」を考えて,外力や支点反力によって部材内部に生じる『内力』を計算します.
言葉で書くと,これだけのことなんですが,これが難しいのですよね.
M図に関しては,「単純梁や片持ち梁のM図は描けるのだけど,門型ラーメンの形になると間違えてしまう(モーメントの描く側が逆になる等)」という質問がよくあります.
「M図の描き方」のインプットのコツを補足で行いますので,M図の描き方に関しては,そちらを参考にしてください.
ポイント2.「「構造物の判別式」は万能ではない!」
「合格ロケット」の01「静定・不静定」項目に進みます.
構造物が安定か不安定か,静定構造物か不静定構造物かに関してですが,この部分に関しても,まずは,広く・浅く勉強しましょう.
テキストなどによっては,外的静定構造物や内的不静定構造物など詳しく説明しているものもありますが,まずは「構造物が安定か不安定か」について判別します.次に,安定構造物に関しては,「不静定構造物なのか静定構造物なのか」に関して判別できるようになりましょう.
その際,「構造物の判別式」を用いる場合があるかと思いますが,この「構造物の判別式」は万能ではないことを覚えておいて下さい.
1層1スパンの構造物に関しては「構造物の判別式」は有効ですが,2層2スパンなどの構造物に関して「構造物の判別式」を適用しようとすると,テクニックが必要になります.
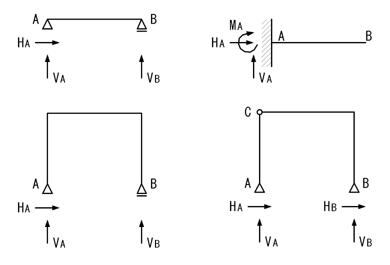
ポイント3.「「静定構造物」の基本形は4パターン!」
「静定構造物」の基本形としては,以下の4パターンがあることを認識してください.
単純梁系や片持ち梁系は,上図のような直線だけでなく,下図の様な形も含まれます.


ポイント4.「「基本的な数値」は覚えてしまおう!」
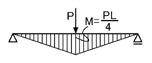
次に01「静定・不静定の解説」の「静定構造物の暗記事項」に関してですが,長さLの単純梁の中央に集中荷重Pが作用する際の,材中央部のモーメントMがM=PL/4であること,及び等分布荷重ωが作用する際の,材中央部のモーメントMがM=ωL^2/8であることは,ぜひ暗記してしまうことをオススメします.
また01「静定・不静定の解説」の「不静定構造物の暗記事項」に関してですが,長さLの両端固定梁の中央に集中荷重Pが作用する際の,材端部におけるモーメント反力MがM=PL/8であること,及び材中央部のモーメントMはM=PL/4-PL/8=PL/8であること,また,等分布荷重ωが作用する際の,材端部におけるモーメント反力MがM=ωL^2/12であること,及び材中央部のモーメントMはM=ωL^2/8-ωL^2/12=ωL^2/24であることは,ぜひ暗記してしまうことをオススメします.
勿論,暗記することが嫌な人は,計算から求めても構いません.
支点反力を「外力系の力の釣り合い」のみでは求めることができないからです.そこで,不静定構造物の問題を解く際には,たわみ角法や固定モーメント法などの解法を使うことになります.合格ロケットでは,固定モーメント法をオススメしております(01「静定・不静定の解説」の「固定モーメント法」を参照).これは「不静定問題」のインプットのコツで補足説明いたしますので,そちらを参考にして下さい.
なお,構造科目が非常に不得意の人は,この不静定問題は「捨て問」扱いにしても結構です.ここで悩むよりは,まずは全体を勉強して,時間的・能力的に余力がある場合には,「不静定問題」のインプットのコツを学習して下さい.
問題コード30041,23041についてですが,初めてこの種の問題を目にした際は非常に難しく感じる問題ですが,解説を一読してください.外力(水平荷重のみの場合がほとんどです)によって,梁に生じる内力(軸方向力,せん断力,曲げモーメント)が,上層から下層に伝わってきます.それぞれの場所で,「力は釣り合っている」ことが理解できるかと思います.
01-1.支点反力
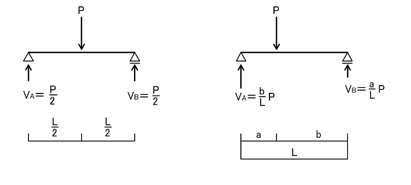
「支点反力」を求めることは静定構造物のほとんどの問題(「静定・不静定」項目に限らず,力学計算問題のかなりの範囲がこの部分に含まれます)において求められます.支点反力の計算を間違えると,その後の計算結果によらずに,間違えた答えを選択してしまうことになりますので,あまり軽視をしないでもらいたいと思います.
集中荷重がかかる問題での支点反力の求め方が基本です.
合格ロケットアプリの解説集00-3「力」の解説②の「反力って何?」「反力の種類」と00-4「力の釣り合い」の解説の「外力と反力との関係(外力系の釣り合い)」を参照してください.
外力が等分布荷重や等変分布荷重(三角形荷重など,下図参照)の場合も,基本は集中荷重の時の考え方です.
■学習のポイント
ポイント1.「等分布荷重や等変分布荷重が作用している場合には,集中荷重に置き換える!」
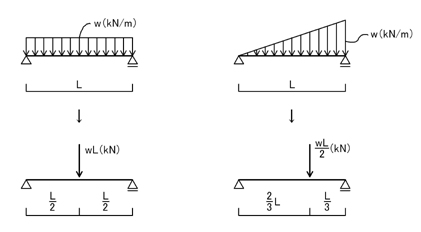
下図の左図ように,「作用対称」の場合は支点反力も左右対称になります.
下図の右図のように「左右非対称」の場合の支点反力は左右対称にはならず,部材の長さに反比例する感じになります.
(下図参照)
00-5「力の流れ」の解説の「「力の発生」のイメージ」と00-6「力の流れ」の解説(補足編)を参照して下さい.
これにより,計算して求めた支点反力のチェックすることができます.
このように,一通りの方法で支点反力を求めるだけでなく,複数の方法で支点反力を求め,クロスチェックすることが重要です.時間があまりかかるわけではないため,クロスチェックすることを強くオススメします.
01-2.M図の描き方
「単純梁や片持ち梁のM図は描けるのですが,門型ラーメンになるとM図が描けない」という話をよく聞きます.話をよく聞くと「M図が描けない」のではなく「M図を間違える」んですね.
N図,Q図に関しては,部材の上に描くのか下に描くのかは重要ではなく,符号が重要です.一般的には,部材の上側や外側にプラス側を描くことが多いですが.
M図に関しては,符号は重要ではなく「部材の引張側に描く」わけです.
そこで,M図の描き方について勉強してみましょう.単純梁を例にとってM図の描き方の基本的な考え方を説明します.
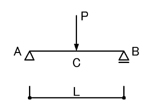
下の図のような単純梁を考えます.
それを,もう少し紐解いてみましょう.
外力として集中荷重Pが単純梁の中央に加わっていますので,支点反力は
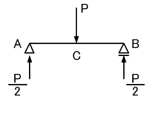
■学習のポイント
例えば,一番上の図のような単純梁において,A-C間やC-B間には外力が加わっていないため,M図は直線になっていますよね.
よってM図を描く際には,M図の線が折れ曲がる点=外力(支点反力も含む)が加わる点におけるモーメントの値と,部材のどっち側が引張になるかについて注意を払えばよいということがわかります.
ポイント2.「ピン支点,ローラー支点にモーメント荷重が加わっていない限り,ピン支点,ローラー支点のモーメントはゼロである!」
これは,00-3「力」の解説②の「反力の種類」を参照してください.
以上により,上記図において,A点のモーメントはゼロであることがわかります.
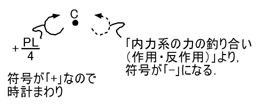
次に,C点に集中荷重Pが加わっていますので,C点のモーメントを求めましょう.
C点をA側(左側)から見た場合について考えましょう.C点をA側からみた場合のC点のモーメントをMCAと表現することとします.
C点をA側(左側)から見るわけですから,下図のように,C点の右側を無視することとします.
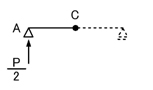
C点の左側には+PL/4(+であるため,時計まわりのモーメントであることがわかります)のMCAが生じているため,「内力系の力の釣り合い(作用・反作用)」よりC点の右側には-PL/4のモーメントが生じていることがわかります.
複雑な形状の問題も,上記考え方でM図は間違えずに描けるようになります.
Q図に関しては,00-8「M図,Q図のイメージ」の解説の「Q図変換」の考え方を用いると,M図からQ図がすぐ求まると思います.
02.断面の性質
この項目の重要ポイントは3つあります.
ポイント1.断面1次モーメント(S)
・02「断面の性質」の解説に目を通してください.考えの基本は,矩形(四角形)の図心位置の求め方です.
・断面1次モーメントは,「足し算・引き算」が可能であることを利用して,L型やT型の図心位置を求めることができるようになってください.
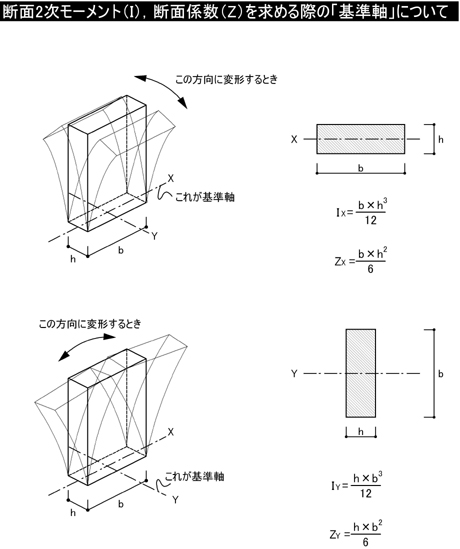
ポイント2.断面2次モーメント(I)
・これは,部材の変形のしにくさを表します.02「断面の性質」の解説にあるように,図心を通る基準軸に関する断面2次モーメントIxがIx=b×h^3/12であることは暗記してしまいましょう.
・「どの軸」に対する断面2次モーメントであるのかに注目してください.
・「足し算・引き算」が可能であるため,□型やI型断面の断面2次モーメントは,分割したそれぞれの図形の断面2次モーメントの和(や差)になることを理解しましょう.
ポイント3.断面係数(Z)
・これは,曲げ強さを表します.図心を通る軸についての断面2次モーメントを図心軸から断面縁までの距離で割って求めることが出来ます.矩形(四角形)の図心を通る基準軸に関する断面係数ZはZ=Ix/(h/2)=b×h^2/6となることを理解しましょう.
・「どの軸」に対する断面係数であるのかに注目してください.
・注意ポイントは,断面係数は「足し算・引き算」が不可能であるため,□型やI型断面の断面係数を求める際には,「□型やI型断面の断面2次モーメント」を計算して,図心軸(基準軸)から縁までの長さで割って計算することを理解しましょう.
・この考えは,03「応力度」の問題などで必要になるために,ここの単元で理解しておきましょう.
補足
断面2次半径(i),断面極2次モーメント(Ip),断面相乗モーメント(Ixy)に関しては,02-1「断面の性質」の解説を一読しておいてください.基本的事項(定義)を覚えておきましょう.
また,「基準軸」という概念を強くイメージしてください.
■学習のポイント
この「断面の性質」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.問題コード18011では,梁A,B,Cがどのように変形するかについてイメージできれば正答肢にたどり着けると思います.特に梁Cに関して変形をイメージできたかがポイントとなりました.
梁Cの変形は,3つのうちの中央部材の中心軸に関して,上部材や下部材が変形するのでしょうか?
上部材は,上部材の中心軸に関して変形しますよね?同様に,下部材は,下部材の中心軸に関して変形しますよね?
この点に着目して,18011を解いてみましょう.
その他の問題については,H型やロ型などの矩形(長方形)以外の断面二次モーメントや断面係数を求めることができるようになっておきましょう!
なお,知っておくと便利な関係として,一辺の長さがDである正方形の断面二次モーメントI□=D^4/12と,直径がDである円の断面二次モーメントI○=πD^4/64の関係として,
I○≒0.6×I□ の関係です.
この関係を知っていると,円の断面二次モーメントの公式を忘れても,大体の大きさを計算することができます.
03.応力度
「応力度」の重要ポイントの説明をする前に,「力」について説明させていただきます.
まず最初に,00-3「力」の解説②~00-6「力の流れ」の解説(補足編)までを一読して下さい.
そうすると,「力」には「外力」と「内力(応力)」という2つの種類があることを理解できると思います.
「外力」とは,物体の外から加わる力のことです.具体的に言えば,例えば単純梁に加わる集中荷重Pや,支点反力などを指します.
一方,「内力」とは,外力によって物体内部に生じる力のことです.外力に応じて生じる力のため「応力」とも言われます.
言葉を変えれば,「外力」が一切加えられなければ(重力なども含む),「内力」は生じません.
ここで,もう一度,00-5「力の流れ」の解説の「作用・反作用の法則」と「内力伝達のイメージ」の部分を読み返してください.
実は,00-5「力の流れ」の部分は,非常にとっつきにくい部分で,この部分が原因で力学計算に嫌気がさしてしまう人が多いです.
なので,「力の流れ」の解説を読み返してみて嫌気がさしてきた人は,あまり深入りせずに次に進みましょう.
力学計算を一通り勉強した後で読み返してみると,意外とすんなり理解できたりしますので,現時点ではあまり心配しないで下さい.
ここで,なぜ「応力度」の勉強をするのかについて,簡単に説明したいと思います.
実際の構造設計において,「許容応力度計算」というものがあります.
概念を説明すると,地震などの「外力」により,部材内部には「内力(応力)」が生じます.その「応力度」が部材材料ごとに決まっている「許容応力度」より小さければ,その部材は「安全」,大きければ部材断面の変更などをしなければなりません.
そのために「応力度」という概念が必要になってきます.そのための勉強であることに気づけば,少しはやる気が起きるかもしれませんね.
「応力」と「応力度」について
「応力度」とは「応力」の「密度」のことを指します.よって,軸方向力が加わった時のように,ある面に一様に「内力(応力)」が生じた場合に部材中の各点に生じる応力度は,「外力」をその点の断面積で割ったものになります(軸方向力なので「垂直応力度」といいます).
生じる「内力」が曲げモーメントやせん断力の場合は,ある面に一様に「内力(応力)」が生じるわけではないので,「垂直応力度」のように「内力(応力)」を断面積で割っただけでは「応力度」は求まりません.
これらについては,以下に挙げる重要ポイントの中で説明させていただきます.
まずは,03-1「応力度」の解説を一読してください.
この項目の重要ポイントは3つあります.
ポイント1.垂直応力度σ(シグマ)
・これは外力により,部材内部に生じる部材方向の「内力(応力)」に関する「応力度」であるため,
垂直応力度(σ)=軸方向力(N)/断面積(A)となります.
ポイント2.せん断応力度τ(タウ)
・これは外力により,部材内部に生じる部材と直交方向「内力(応力)」に関する「応力度」であるため,
平均せん断応力度(τ)=せん断力(Q)/断面積(A)となります.
・せん断応力度(τ)は,垂直応力度(σ)と異なり,応力度は部材断面内に一様に発生しません.矩形断面(四角形断面)や円形断面におけるせん断応力度の分布は断面の中央部が最大となり,縁の部分ではゼロとなります.
・矩形断面における最大せん断応力度(τ)はτ=3/2×Q/A,円形断面における最大せん断応力度(τ)はτ=4/3×Q/Aとなります.
ポイント3.曲げ応力度σb(シグマビー)
・曲げモーメントを受ける部材は,中立軸を境に圧縮側,引張側に分かれます.曲げ応力度は中立軸上でゼロとなり,中立軸から遠ざかるほど大きくなるため,部材断面上下縁で最大となります.これを「縁応力度」と呼び,「曲げ応力度」とは基本的に「縁応力度」のことを指すため,曲げ応力度(σb)=曲げモーメント(M)/断面係数(Z)となります.
・なぜ,曲げモーメントを断面係数で割ると曲げ応力度になるのかは,「全塑性モーメント」のインプットのコツの中で解説させていただきますので,現時点では,そのまま覚えてしまいましょう.
断面内部に生じる「応力度」をすべて足すと,外力によって生じる軸方向力・せん断力,曲げモーメントなどの「応力」になります.
言葉を変えると,軸方向力・せん断力,曲げモーメントなどの「応力」を面積あたりに分解すると「応力度」になります.
これら3つの重要ポイントに注意を払い,過去問題を解いてみましょう.
このように「現象を数式化し,関係式を導き出す」ことが,力学計算編を得点源にする最大の要因の一つであることを理解してください.
次に,過去に出題されたことのある2軸曲げについて,補足説明させていだたきます.
偏心荷重という言葉を聞いたことがありますか? 偏心荷重とは,
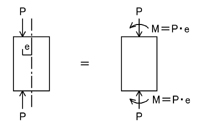
のように,部材には外力として軸方向力である集中荷重Pしか加わっていないのに,外力の加わっている位置によって,部材には集中荷重Pの他に,集中荷重Pによって生じる曲げモーメントも同時に外力と加わっているとみなせるような集中荷重Pを指します.
上記左右の図に生じる内力(応力)が同じものになる,言葉を変えれば,左右の図が=で結ばれることが理解できるようになればしめたものです.
この問題は,「2軸曲げの問題」といい,「応力度」の問題の中では最も難しい問題です.部材の端部に外力Pが加わることにより,ニ方向に変形が進む(3次元的変形)問題だからです.
余り深入りせず(現時点で理解できなくてもいい難しい問題です),一通り勉強が終わった際に,余裕があれば見直せばよい問題(通称:捨て問)の一つです.
2軸まげの問題を捨てない人のために,補足説明を続けますが,
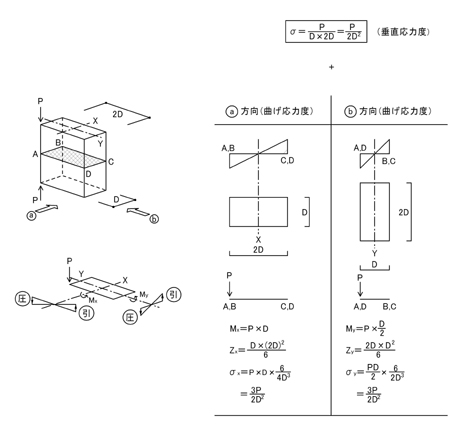
a方向から見た場合,外力Pによって断面の左側(A点,B点側)が圧縮,断面の右側(C点,D点側)が引張になります.同様に考えると,b方向から見た場合,外力Pによって左側(A点,D点側)が圧縮,断面の右側(B点,C点側)が引張になることがわかります.
以上より,圧縮応力度をマイナス,引張応力度をプラスとした場合,A点からD点のうち,A点に生じる応力度が最も小さく(a方向から見てもb方向から見ても圧縮側なので),C点に生じる応力が最も大きく(a方向から見てもb方向から見ても引張側なので)なると判断することができます.
各点に生じる応力度の具体的な値は上記ポイント1.とポイント3.より計算できます.
この「応力度」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.
04.全塑性モーメント
部材に曲げモーメントMのみがかかる場合の,部材内部の「応力」状態を見ていきましょう.
これは,「微小変形理論」や「平面保持の仮定」というものに基づいているからなんですが,こんな言葉「微小・・・」などは知らなくてもいいです.部材中央に曲げモーメントMを受ける場合,圧縮側の縁応力度も引張側の縁応力度も同じ大きさになることは感覚的に理解できると思います.
この曲げモーメントが少しずつ大きくなると,圧縮側,引張側共に,縁応力度が降伏応力度σy(部材材料ごとによって異なります)に達します(上記図の二番目の図).ココまでが弾性範囲です.
降伏応力度σyとは,部材材料が降伏する(壊れてしまう)応力度であるため,更に曲げモーメントMが大きくなると,三角形(三角柱)の応力状態を保てなくなります.上記図の三番目の図のように,台形のように応力状態が進んでいきます.更に曲げモーメントMが大きくなると,上記図の一番下の図のようになります.これ以上は増えようがないので,上記図の一番下の図のような応力状態を「塑性状態」といい,塑性ヒンジが生じることになります.塑性ヒンジに関しては,「崩壊荷重」のところで説明します.
ここで,00-3「力」の解説②「モーメントって何?」「モーメントの計算」,00-5「力の流れ」の解説の「力の発生のイメージ」を一読して下さい.
つまり,「モーメント」とは,「大きさが同じ」で「向きが逆」の一対の集中荷重(「偶力」と言います)に置き換えて考えることが出来ます.
もう少し具体的な例で説明しますと,自動車の運転の「ハンドル」や水道の「蛇口」を思い出してください.
自動車の運転で右折する際には,ハンドルを時計廻りに回します.実際には,左腕を上に,右腕を下に動かすことで,ハンドルは時計廻りに回ります.
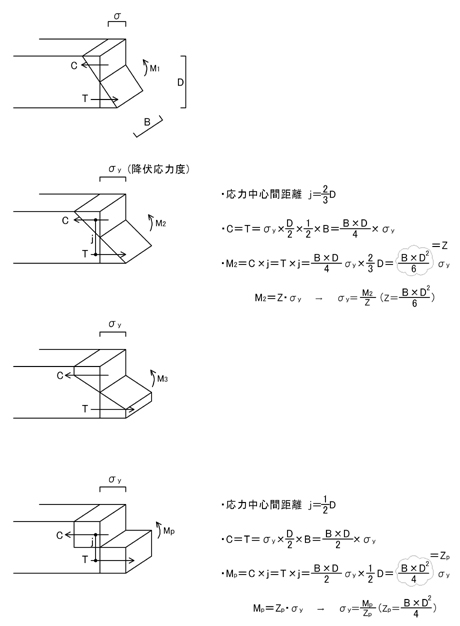
曲げモーメントM2を受ける部材(上記図の上から二番目)でも,同様に,曲げモーメントM2を圧縮合力Cと引張合力Tという,「大きさ同じ」で「向きが逆」の一対の力(偶力)で置き換えて考えることができます.
弾性範囲内で考えた場合,圧縮合力Cや引張合力Tの大きさは,三角柱の体積に相当します.よって,C=T=σy×D/2×1/2×Bとなることが理解できるかと思います.
偶力の距離(応力中心間距離といいます)をjとすると,M=C×j=T×jとなるため(これは,00-5「力の流れ」の解説の「力の発生のイメージ」参照),上記図の二番目の図横に書いてあるように,M2=B×D^2/6×σyとなります.
「応力度」のインプットのコツで,曲げ応力度σbとは,曲げモーメントによって生じる「応力度」であるため,σb(σy)=M2/(B×D^2/6)となっていましたよね.σb=M/Zと比較すると,Z=B×D^2/6となることが理解できると思います.
塑性状態(上記図の一番下の図)の場合,圧縮側,引張側ともに応力状態は三角形(三角柱)ではなく四角形(四角柱)になるため,圧縮合力C,引張合力Tはともに,上記図の一番下の図横に書いてあるように,C=T=σy×D/2×B=B×D/2×σyとなります.これら偶力の距離jは,j=D/2となります(これは,上記図の一番下の図より理解できますよね).
塑性状態の時のモーメントを全塑性モーメントといい,Mpと記すとします.そうすると,Mp=C×j=T×j=B×D/2×σy×D/2=B×D^2/4×σy・・・①と計算できます.
部材断面が塑性状態であるときの断面係数を塑性断面係数Zpと記すと,弾性状態の時と同様に,Mp=Zp×σy・・・②と表すことができます.
①と②式を比較すると,Zp=B×D^2/4となります.これは,覚えてしまいましょう.
この項目の重要ポイントは2つあります.
ポイント1.塑性断面係数Zpは足し算・引き算が可能である.
「断面の性質」のインプットのコツで説明しましたが,弾性状態の断面係数Zは,足し算・引き算できません.でも,塑性断面係数は足し算・引き算が出来ます.これは,覚えてしまいましょう.
ポイント2.部材に曲げモーメントMと軸力Nの両方がかかる場合の解き方です.
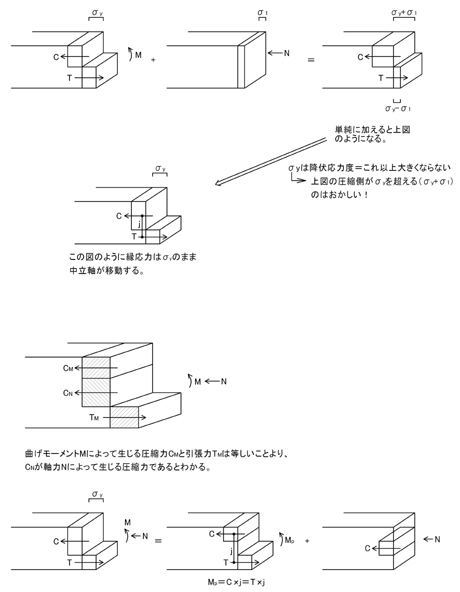
部材に曲げモーメントMと軸力Nの両方がかかる場合には,上の図の上段に並んでいる3つの図の右側のように縁応力がσyを超えるような応力状態は起きずに,実際は,その下の図のように,縁応力はσyのまま,中立軸(圧縮領域と引張領域の切り替わる部分)が移動します.
言葉を変えると,縁応力はσyを超えることができないので,上記上から2段めの図のように,曲げモーメントMと圧縮軸力Nが両方かかる場合は,圧縮側の応力場(四角柱の体積)が大きくなるわけです.
曲げモーメントは偶力で表すことができましたよね.偶力とは,「大きさが同じ」で「向きが逆」の一対の集中荷重であるため,曲げモーメントMによって生じた圧縮合力CMと引張合力TMは同じ大きさになります.
残りの圧縮合力が軸力Nによって生じた圧縮合力CNと考えることができます.
まずは,基本となる矩形断面の24011で,「基本的な問題の解き方」をマスターしてしまいましょう.
その次には,22011,02011,25011のようなH型や,28011,30011のようなロ型をマスターしていきましょう!
■学習のポイント
この「全塑性モーメント」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるので,得点源にしてしまいましょう!
05.崩壊荷重
この項目に対して「難しそう・・・」というイメージを持っている人が多く見られます.が,実は,得点源の項目です.
以下に説明する重要ポイントを理解すれば,得点源になります.頑張りましょう!
まず最初に,言葉の説明をします.
・崩壊:単純梁やラーメンなどの構造物に荷重を作用させ,その大きさを増大させていく時,それ以上の荷重を加えなくても「ただ変位のみが増大して」変形を生じる状態
・崩壊荷重:崩壊の生じる時の荷重
・崩壊機構:構造物に塑性ヒンジが形成され,その構造物が不安定な状態になるメカニズム(機構)
・塑性ヒンジ:部材のある断面が全塑性モーメントに達して,回転自由なピン状態になった部分
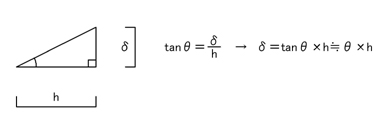
次に,『学科試験の「崩壊荷重」の問題を考える時の回転角θはすごく小さい時を考える』という前提条件に基づいていることを覚えておきましょう.それによって,回転角θがすごく小さい時は,tanθ≒θとみなすことができるんです.このことも覚えておいて下さい.
ここで,「合格ロケット」に収録されている05-1「崩壊荷重」の解説を一読して下さい.
この項目の重要ポイントは5つあります.
ポイント2.仕事(量)=力×移動距離
単純梁やラーメンなどの構造物に外力Pを加えていくと,構造物に内力が生じます.外力が増えるにつれ,内力も増えていきます.一番弱い部材が塑性状態になります(塑性ヒンジが発生します).
具体的な問題の解き方は,「外力による仕事」と「内力による仕事」が等しいという点に着目します.
「外力による仕事」とは,外力Pによって,材が変形します.その仕事量(=力×移動距離)を指します.
「内力による仕事」とは,外力Pによって,材に内力が生じます.構造物が崩壊機構に達した時に,部材に塑性ヒンジが発生して,部材が回転します.その仕事量(=部材の塑性モーメント×回転角)を指します.
ポイント3.塑性ヒンジは部材の弱い方に発生します.
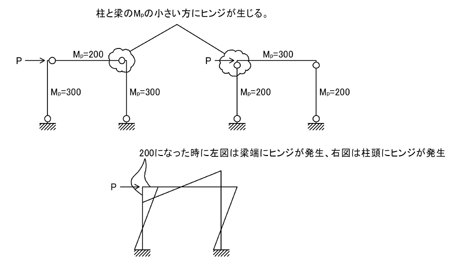
上記左図では,梁の塑性モーメントが200,柱の塑性モーメントが300であるため,外力Pによって柱と梁に生じる内力(曲げモーメント)が200に達した時点で,柱ではなく梁の方に塑性ヒンジが発生します.
ポイント4.柱の長さが異なるラーメン構造物の「外力」による柱の移動距離の求め方
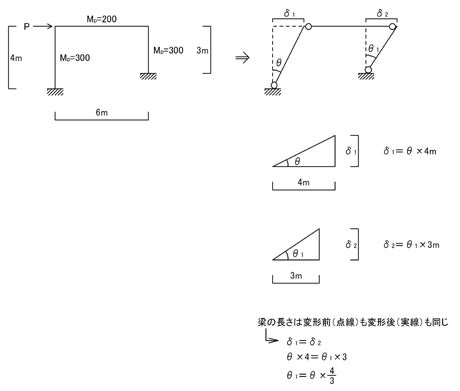
ポイントは,梁の長さは,変形前も変形後も変化しないことです.
ポイント5.「内力による仕事(=部材の塑性モーメント×回転角)」は『新たに発生したヒンジに関してのみ』考慮すること
例えば,片側が固定端,もう一方がピン支点であるラーメン構造物の場合,ピン支点の部分に関しては,元々ピンであり,塑性ヒンジが発生したわけではないので,「内力による仕事」とは考えません.
以上の重要ポイントに意識して,過去問を解いて見ましょう.
■ 学習のポイント
一番最初の部分に書きましたが,この「崩壊荷重」という項目に苦手意識を持っている人は多いのですが,意外と点数が取りやすいと思えるようになりませんか?もう一度,解説に目を通してください.
この「崩壊荷重」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットアプリに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できますよ!
06.トラス
学科試験における「トラス」の問題は,以下の仮定に基づいています.
・全ての部材が直線で,三角構成された骨組み
・節点が全てピン接合
・外力(集中荷重のみ)は節点にのみ作用
ポイント1.「節点には曲げモーメントは生じない.各部材に生じる応力は軸力のみ!」
上記,仮定に基づいているため,ポイント1.が言えます.それによって,問題を解くという行為が容易になるわけです.
次に,問題を解くという行為をより容易にするために
ポイント2.「ゼロ部材を探せ!」
「ゼロ部材」とは,応力(軸力)が生じない部材のことです.「トラス」の問題は,ある外力がかかる構造物において,ある部材に生じる応力はいくつになるでしょう?という問題ですから,「ゼロ部材」を探しだし,その部材を無視して考えると,より容易になります.
具体的には,節点に2つの部材が接合されていて,その節点に外力(反力)が作用していない場合には,その2つの部材に生じる応力はゼロである.ということが言えます.
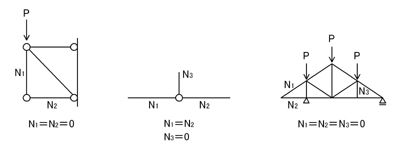
建築士の学科試験のトラス構造物の問題は,「力は釣り合っている」わけです.「外力(反力)」も,それによって生じる「内力(軸力)」も釣り合っているわけです.例えば,上記図の真ん中の図において,N3がゼロでなければ,N3の内力に釣り合う力が存在しません.N1に関しては,「大きさが同じ」で「向きが逆」であるN2と釣り合うことで,「力の釣り合い」は成立できます.つまり,N3=0と考えることができます.
実際に問題を解く際に,「ゼロ部材」を鉛筆などで塗りつぶしてみると,部材数が減って,問題が簡単になります.
ポイント3.「切断法」「節点法(示力図は閉じる)」をマスターしよう!
トラス構造物では,上記の仮定に書いてあるように,「軸力しか生じなく」かつ「内力も釣り合っている」ため,問題解法として「節点法(示力図は閉じる)」という方法が使えます.これは,06-1「トラス」の解説内の『部材に生じる軸力を求める場合,節点ごとに考えていく』に説明してあります.また「切断法」に関しては,06-1「トラス」の解説内の『Nfgを違う解法で求める』に説明してあります.
ここで,
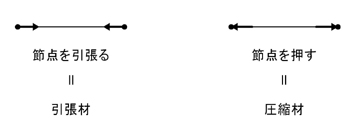
引張材と圧縮材は,上記図のようにルール付けします.逆に考える人も多くいるので注意して下さい.
「トラス」の問題の基本的な解き方としては(静定構造物であるので),「外力系の力の釣り合いを考える」→「内力系の力の釣り合いを考える」という2つの計算しかありません.
「外力系の力の釣り合い」とは,「外力(集中荷重)」によって,「支点反力」生じます.それを求めることを指します.
「内力系の力の釣り合い」とは,「外力(集中荷重)」によって生じた「内力(軸力)」を求めます.「節点法(示力図は閉じる)」や「切断法」によって求めることを指します.
「切断法」のポイントとしては,
・「切断する部材」は3つ以下
・具体的な計算としては,ΣM=0,あるいはΣY=0のどちらか
となります.
03051と21051について補足説明させていただきます.
通常のトラスの問題は「部材○○に生じる軸方向力はいくつか」という問題文であるのに対し,この問題は「ローラー支点の水平方向(横方向)の変位δBはいくつか」という問題ですね.
この問題を見たときに「通常のトラスの問題とは違うぞ.どうしよう??」と思った後で,「んん?求めたいのは水平変位δで,『それぞれの部材は等質等断面とし,断面積をA,ヤング率をEとする』の部分って,どこかで見たことがあるぞ!」という風に考えられるかがポイントです.
『ひずみ度ε(イプシロン)とは,長さLの部材が外力PによってΔLだけ変形した際に,ε=ΔL/Lと定義するものです.
ヤング係数Eとは,外力がかかった際の部材の変形のしにくさを表す指標であり,ヤング係数(E)=垂直応力度(σ)/ひずみ度(ε)で表現することができます.式を変形すると,垂直応力度(σ)=ヤング係数(E)×ひずみ度(ε)と表すこともできます.
部材にかかる外力(軸方向力)をN,部材断面積をAとすると,外力Nにより部材に生じる内力(σ)はσ=N/Aと表すことができるので,N/A=E×ΔL/L,これより,ΔL=NL/EAとなります.
このように「現象を数式化し,関係式を導き出す」ことが,構造(力学計算編)を得点源にする最大の要因の一つであることを理解してください.』
の部分が思い出されるかが解ける,解けないの分岐点になることがわかると思います.
「節点法」のポイントに関しては,「節点法」のインプットのコツを参照して下さい.
■ 学習のポイント
この「トラス」については,本試験においては,過去問題の類似問題が出題される傾向にありますので,今年度の本試験問題においても合格ロケットに収録されている過去問20年分で問われた知識をきちんとマスターしてさえいれば確実に得点できるものと考えます.
しかし,上記「トラス」の3つの重要ポイントを駆使しても考え方がわからない問題は,一番後回しにすることを薦めます.
06-1.節点法の解き方
トラス構造物の問題を解く方法に,切断法と節点法の2種類があります.更に節点法の中には,数値計算法と図式法の2種類があります.
その節点法の中の図式法のことを「示力図は閉じるで解く方法」と呼ぶこともあります.
今回は,この図式法について説明します.
まず,前提条件として,トラス構造物の問題は静定構造物であることがあります.ということは,力は釣り合っているわけです.
外力系の力の釣り合いで考えるとトラス構造物全体に関して,力は釣り合っていることがわかります.
内力系の力の釣り合いで考えると,トラス構造物全体が釣り合っているためには,各節点も釣り合っていることになります.
そこで,各節点ごとに,内力系の力の釣り合いを考え,力は釣り合っていることを数値計算ではなく図解法として行う方法に図式法は位置します.
それでは具体例で説明していきましょう.
下図の問題で説明していきます.
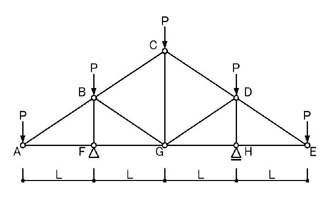
のような問題です.
静定構造物であるため,外力系の力の釣り合いを考え,支点反力を求めます.
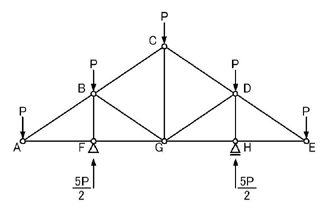
のようになります.
次に,ゼロ部材を探します.ゼロ部材に関しては「トラス」のインプットのコツのポイント2.を参照してください.
この問題の場合は,セロ部材はありませんね.
ポイント1.図式法では,未知力が2つ以下の節点について,力の釣り合いを考える!
このポイントは覚えてください.
なぜなのでしょうか.
簡単に言うと,未知力が3つ以上の節点について力の釣り合いを考えてみても,解くことができないからです.
上図において,左右対称であるため,左半分について考えます.
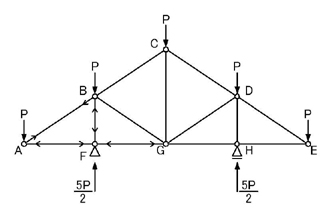
A点,B点,C点,F点,G点のうち,未知力が2つ以下の場所を考えます.
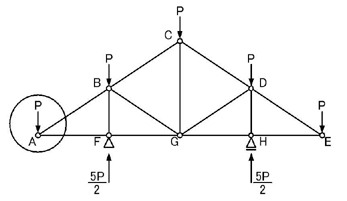
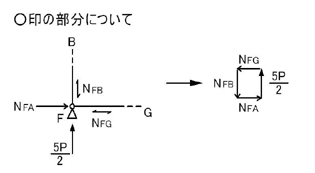
A点の未知数が2つですので,A点について考えてみましょう.
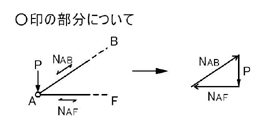
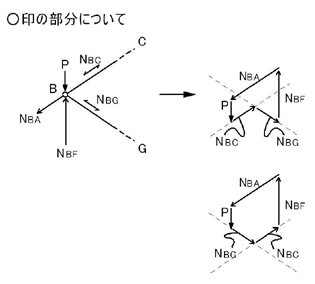
「節点で力が釣り合っている」=「示力図は閉じる」わけなので,節点Aに加わる力(外力P,NAB,NAF)の始点と終点とを結ばれる一筆書きができるように力の足し算を行います.上図の右図ですね.
つまりA点での力の釣り合いは上図のようになります.
NABは節点を引張る方向の力であるため引張力で,NAFは節点を押す方向の力であるため圧縮力であることがわかります.
それを,問題の図に記入してみます.
のようになります.AB材は引張材であることがわかり,B点に関してNBAは節点を引張る方向に生じていることがわかります.同様に,AF材は圧縮材であるとわかり,F点に関してNFAは節点を押す方向に生じていることがわかります.
続いてB点,C点,F点,G点において,未知力が2つ以下の部分を探します.
F点が該当しますね.
F点について力の釣り合いを考えて見ます.
上図の左図にあるような各力が閉じるようになるためには,上図の右図のような力の向きであればよいことがわかります.
以上により,F点に関しては,上図のような力の釣り合いが成り立つことがわかります.
これを問題の図に記入しましょう.
のようになります.
次にどの点について考えればよいでしょうか.
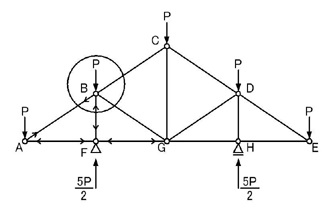
B点ですね.
上図の左図のような各力が閉じるようにするためには,どうすればよいでしょうか.
上図の右図の上図でも下図でも閉じていることがわかります.
好きな方でいいので,各力が閉じるときの,各力の方向を自分で求められるようになってください.
以上の図より,NBCはB点を引張る方向の力,NBGもB点を引張る方向の力であることがわかります.
これを,問題の図に記入します.
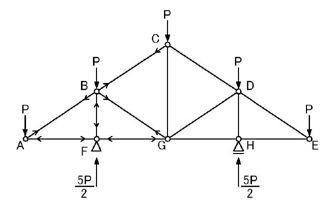
のようになりますね.
この問題は架構も外力も左右対称であるため,各部材に生じる応力も左右対称になることはイメージできるでしょうか.
そうすると,
のようになります.
続いて,C点に関して力の釣り合いを考えて見ましょう.
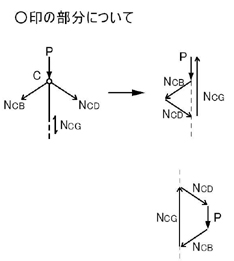
上図の左図にあるような各力が閉じるようになるためには,上図の右図のような力の向きであればよいことがわかります.右図の上図でも下図でも閉じていればいいのですから,どっちでも構いません.
どちらの示力図でもNCGはC点を押す力(圧縮力)であることがわかります.
これを問題の図に記入すると
のようになります.
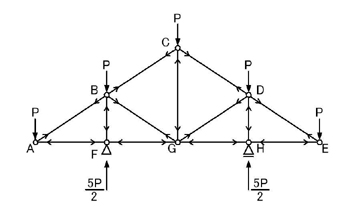
以上のことにより,「節点法」で各部材に生じる軸力が引張力か圧縮力であるかが判別することができます.
この問題のように,引張材か圧縮材かという問題に関しては,節点法の図式法で求めることができます.
しかし,ある部材に生じる軸力の値を求める問題に関しては,各節点での力の釣り合いを考えるときに,各力の値も求めなければなりません.
その際,「三四五の定理」や「ピタゴラスの定理」などの知識が必要になってきます.その辺は,00基礎知識の解説を参照してください.
また,図式法で各節点での力の釣り合いを考えるときに,例えば上記問題のC点におけるNCGと外力Pのように,向きが逆の力が出てくる場合に,各力の大きさの大小関係がわからないと,図式法で上手く示力図を描けない場合があります.
その時は,例えば上記問題のように全ての部材の長さがわからない場合,あるいは,角度が分からない場合には,各自で適当に決めてしまう方法があります.
例えば,
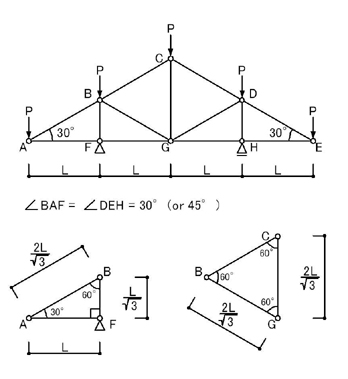
のように,∠BAF=30°であるとか,CG材の長さをLとかにして,「三四五の定理」や「ピタゴラスの定理」の定理を使いながら図式法で求めていく方法です.
この節点法に関しては,非常に多くの質問が来ます.また,各節点に関する示力図をまとめた「クレモナ図」についても質問が来ます.
ですので,「節点法を機械式に解く方法」という資料を作成しましたので,目を通しておいて下さい.【こちら】
■学習のポイント
トラス構造物として,図式法にとらわれ過ぎないように注意して下さい.問題によっては,切断法の方が簡単に求めることができます.切断法,図式法ともに解法を理解した上で,自分で使い分けられるようになってください.使い分けられるようになるためには,過去問で練習する方法が非常に有効です.
07.たわみ
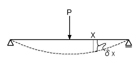
部材に外力が作用し変形した時の部材中の任意の点の変位量を「たわみ」といいます.下図において,X点におけるたわみをδx(デルタエックス)といいます.
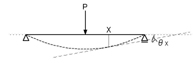
部材に外力が作用し変形した時の変形後の部材の任意の点における接線と,部材軸とのなす角度を「回転角」または「たわみ角」といいます.下図において,X点における回転角をθx(シータエックス)といいます.
この項目において,単純梁,片持ち梁,両端固定梁の部材中央部分に集中荷重Pが加わる形と部材全体に等分布荷重ωが加わる形,及び片持ち梁の先端にモーメント荷重Mが加わる形を「たわみ及び回転角の基本形」と呼ぶことにします.
これらのたわみや回転角を計算で求めようとする場合には,積分計算が必要になってきます.
そこで,微分・積分計算が苦手な人は「基本形」のたわみと回転角は暗記してしまいましょう!
暗記する項目をなるべく減らしたい人は,「モールの定理」のインプットのコツ内で,計算によりたわみや回転角を求める方法を説明いたしますので,そちらを参考にしてください.
ポイント1.「たわみ」「回転角」の基本形は覚えよう!
具体的には,下図に示す12個の数値を覚えることになります.

続いて,知っていたらたわみが楽に求められる知識として「マクスウェルの定理」というのがあります.
ポイント2.マクスウェルの定理を知っておこう!
「A点に荷重Pが作用する時のB点のたわみδBと,B点に荷重Pが作用する時のA点のたわみδAが等しくなる」という定理です.
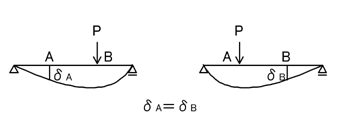
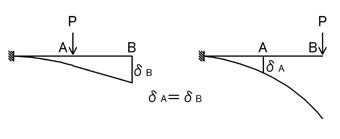
ここで,過去問題を見てみましょう.上記「基本形」の数値を暗記しておけば対応可能ですね.
なお,「モールの定理(その2)」のインプットのコツの中で,「モールの定理の元になっている考え方」という積分を用いてたわみや回転角を求める方法に関して説明してある部分があります.この部分を勉強すると,たわみδとモーメントMやせん断力Qとの関係が理解できると思います.
しかし,この部分は数学の計算が得意な人以外は,あまり深入りしてはいけない危険な世界です.微分・積分などを用いた計算を行ってもいいから暗記項目を極力減らしたい人は,「モールの定理」のインプットのコツを参照して下さい.
過去問題について追加説明させていただきます.
問題コード19021,27021の問題は非常に難しいです.これらは「基本形」だけでは太刀打ちできないような問題です.
「事象を具現化する」ことを求められている訳です.
具体的には,「問題の架構がどのような挙動を示すか(変形をするのか)」を考え,「自分の持っているパーツ(インプットのコツで説明している各項目の重要ポイント)で対処できないか」について考えなければならないわけです.
この部分が,「たわみ項目の問題はいくらでも難しい問題を出題することが可能だよ」という背景でもあります.
構造を苦手としている人は,まずは,問題コード19021及び27021の問題はパスして先に進みましょう.全体の勉強を終えてから余裕があれば,再度チャレンジしてみてください.
■ 学習のポイント
この「たわみ」については,インプットのコツで説明してある「基本形」のたわみと回転角を求めることを,確実に行えることができるようになっておいてください.その上で,問題コード19021や27021のように,「基本形」に関する知識だけでは太刀打ちできない場合は「全体挙動を考える」→「その挙動の中に,基本形が含まれていないかについて考える」というような考え方をするようにしてください.
再度繰り返しますが,建築士の学科試験は満点を取らなくても受かることができる試験です.たわみ項目の難しい問題にとらわれ過ぎて,他の問題が時間切れになるようなことが起きないように気をつけてください.
07-1.モールの定理(その1)
単純梁や片持ち梁に集中荷重やモーメント荷重が加わるときの部材の「たわみ」や「回転角(たわみ角)」を求める方法に「モールの定理」があります.
「モールの定理(その1)」のインプットのコツでは,まず最初に,単純梁と片持ち梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法を説明します.
「モールの定理(その2)」のインプットのコツでは,部材端部以外に支点がある架構や連続梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法を説明します.続いて,「モールの定理の元になっている考え方」他に関して説明します.
「モールの定理」の基本として,
ポイント1.「各点の回転角は,弾性荷重によるその点のせん断力Qに等しい」「各点のたわみは,弾性荷重によるその点のモーメントMに等しい」
ポイント2.「ピン支点,ローラー支点はそのまま」「固定端は自由端に,自由端は固定端に変更する」
があります.
ここで,「弾性荷重」とは,(梁に生じる)曲げモーメントMを,その梁の曲げ剛性EIで割ったM/EIのことを指します.
言葉だけではイメージし難いので,具体例を用いて説明していきましょう.
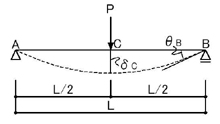
上図のような単純梁のC点におけるたわみδC,B点における回転角θB(A点における回転角θA)を求めてみましょう.
手順1.M図を求めます.M図は下図のようになりますね.
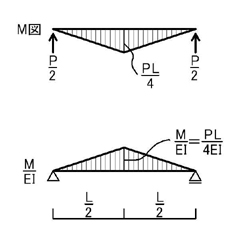
手順2.上図のように,部材中の各点に発生する曲げモーメントMをEIで割った数値をM図が発生する側と逆側に荷重(弾性荷重)として作用させます.
この時に,ポイント2.に注意しましょう.上図の問題では,単純梁であるため,ピン支点とローラー支点しかないため,支点の変更はありません.
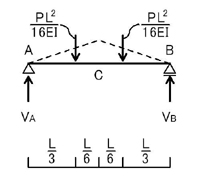
外力系の釣り合いは上図のようになるため,支点反力VA=VB=PL^2/16EIとなります.
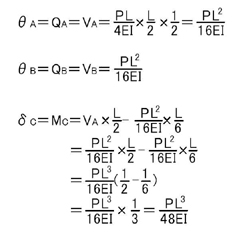
よって,A点における回転角θA,B点における回転角θB,C点におけるたわみδCは
続いて,片持ち梁の先端に集中荷重が加わるときについて考えて見ましょう.
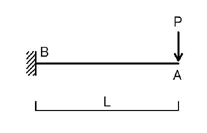
のような場合ですね.
手順は単純梁の場合と同様です.
M図は下図のようになりますね.
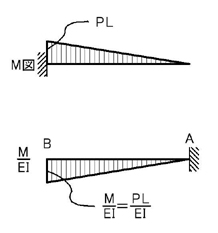
MをEIで割った弾性荷重を作用させた場合を考えて見ましょう.
ポイント2.に注意しましょう.「固定端は自由端に,自由端は固定端に変更する」とは,具体的には上図のように,弾性荷重を考えるときに,支点の状態を変更して考えることを指します.
この三角形の弾性荷重は,
のように,集中荷重に置き換えて考えて見ましょう.重心位置に三角形の面積分の荷重がかかると考えればいいのです.
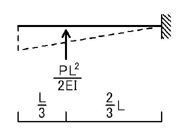
そうすると,A点の回転角θA,B点の回転角θB,A点のたわみδAは

のようになります.問題の図において,B点は固定端であるため,B点の回転角はゼロになるのは理解できますね.
続いて,下図のように,片持ち梁の(先端以外の)ある点に集中荷重が加わるときについて考えて見ましょう.
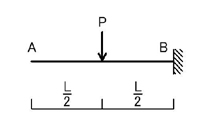
M図は下図のようになります.
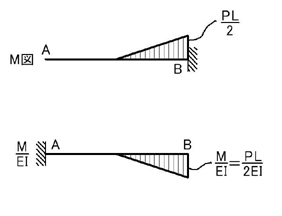
弾性荷重を考えると上図のようになることがわかると思います(支点の変更に注意!).
下図のように,三角形荷重を集中荷重に置き換えて考えると
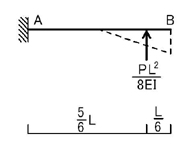
A点,B点の回転角とA点のたわみは
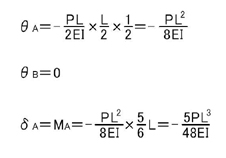
のようになります.
続いて,モーメント荷重が加わるときについて考えて見ましょう.
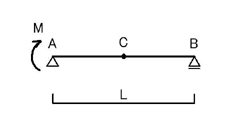
上図のような問題ですね.
モーメント荷重が加わる場合の考え方は,集中荷重が加わるときと同様です.
まずは,モーメント図を考えましょう.
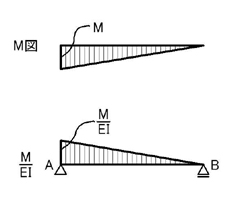
上図のように,弾性荷重を考えます.この問題の場合は,単純梁であるため,ポイント2.の支点の変更はありません.
ポイント1.より,A点,B点のせん断力QA,QBを求める(=支点反力VA,VBと同じ値になります)ことにより,A点とB点の回転角θAとθBが求まります.C点のモーメントの値MCを求めることで,C点のたわみδCが求まります.
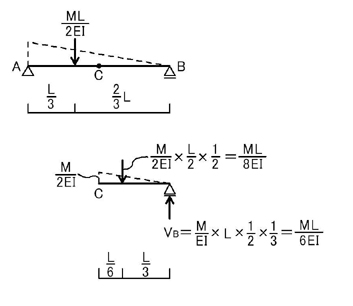
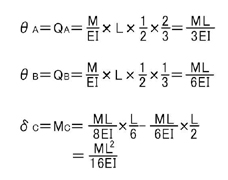
次に,この問題におけるたわみが最大の点のたわみδmaxを求めてみましょう.
δmaxはθ=0の位置であることは理解できるでしょうか.
単純梁の部材中央に集中荷重が加わる場合(このインプットのコツの一番上の図参照)を考えて見ましょう.
部材中央のC点のたわみが最も大きいことは理解できると思います.この図において,端部(A点,B点)の回転角θAとθBが最も大きく,中央部C点の回転角θCはゼロであることがわかるかと思います.
ポイント3.たわみの最大値は,回転角がゼロとなる位置で生じる!
では,単純梁にモーメント荷重が加わる場合のδmaxを求めてみましょう.
下図のように,弾性荷重を考え,B点から任意の点(B点から距離xだけ離れた点をx点とします)でのせん断力Qxを計算します.
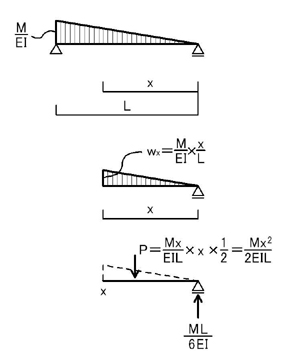
上図のように,x点より右側を考え(左側でも構いません)ます.B点の支点反力は上向きにML/6EI,弾性荷重のうち,今回対象範囲(x点から右側の部分の三角形)を集中荷重に置き換えて考えるとP=Mx^2/2EILとなります.
よって,x点でのせん断力Qxは
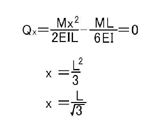
となり,δmaxはB点よりL/√3の位置で生じることがわかります.
下図のような片持ち梁にモーメント荷重が加わるときについてはどうでしょうか.
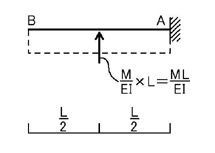
M図は下図のようになり,
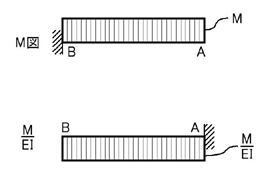
弾性荷重M/EIは上図のようになりますね.
A点でのせん断力QAはM/EIとなり,A点でのモーメントはML^2/2EIとなることが理解していただけると思います.
以上の説明は理解できましたでしょうか.
「モールの定理(その1)」のインプットのコツでは,単純梁や片持ち梁に集中荷重,モーメント荷重が加わる場合の「モールの定理」の計算方法について説明しました.
通常のテキストなどでは,「モールの定理」とは,単純梁と片持ち梁を対象とした説明になっていると思われます.しかし,この考え方を拡張すると,架構の中間に支点のある架構にも適用することができます.
それについては「モールの定理(その2)」のインプットのコツで説明します.
07-2.モールの定理(その2)
単純梁や片持ち梁に集中荷重やモーメント荷重が加わるときのモールの定理による計算方法に関しては,「モールの定理(その1)」のインプットのコツを参照して下さい.
今回は,単純梁,片持ち梁以外の架構にモールの定理を使う場合について考えて見ます.
まずは,連続梁の解き方について考えて見ましょう.連続梁とは,下図のように,ピン接合点や連続梁の支点を持つ架構を指します.
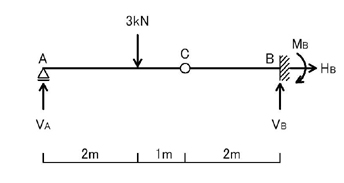
ここで,支点についてまとめてみましょう.
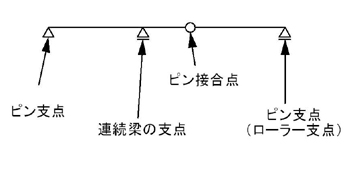
ピン支点,ローラー支点は,単純梁と同様です.部材端部に位置することに注意して下さい.
特徴としては,「反力が生じる」かつ「モーメントは生じない」ことが言えます.
連続梁の支点というのは,部材端部以外にあるピン支点,ローラー支点を指します.
特徴としては,「反力が生じる」かつ「モーメントが生じる」ことが言えます.
ピン接合点というのは,部材端部以外にあるピンを指します(ピン支点ではありません).
特徴としては,支点ではないので「反力は生じない」かつ「モーメントは生じない」ことが言えます.
ポイント1.「ピン支点」「連続梁の支点」「ピン接合点」の違いを理解しよう!
連続梁の問題の解き方は,
ポイント2.ピン接合点(上図C点)のところで切断し,単純梁と片持ち梁として解いていく!
上図のように,まず,ピン接合点(上図C点)で左右に分けて考えます.
左図を単純梁とみなして支点反力を求めます.VA=1kN,VC=2kN(共に上向き)となります.
しかし,C点はピン接合点であり,支点反力は生じないため,上図の右図のC点に下向きのVCを加えてあげることで,C点には支点反力が生じていないことになります.
その結果,VB=2kN(上向き),HB=0,B点での外力系の力の釣り合いを考えると,MB-VC×2=0→MB=2VC=4kN・mとなります.
連続梁は以上のように解くことができます.
それでは,本題に入ります.
「モールの定理(その1)」のインプットのコツのポイント2.で「弾性荷重を考える手順において,支点条件を変更する」ということが必要であると説明しました.
「ピン支点,ローラー支点はそのまま」「固定端は自由端に,自由端は固定端に変更する」わけです.
「モールの定理(その2)」のインプットのコツでは,更に以下の支点条件の変更を考慮することにします.
ポイント3.「連続梁の支点はピン接合点に,ピン接合点は連続梁の支点に変更する!」
モールの定理を用いて問題を解く際の手順は,単純梁や片持ち梁の場合と同様です.
では,具体的に解いていきましょう.
手順1としてモーメント図を描くわけですから,まず最初に支点反力を求めましょう.
計算は省略しますが,上図のような支点反力が求まります.
そうすると,モーメント図は
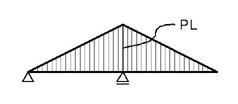
のようになります.
続いて,弾性荷重について考えましょう.
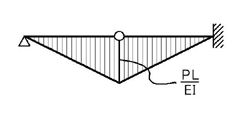
弾性荷重の最大値は,モーメント図の最大値PLをEIで割ったPL/EIとなりますね.また,A点のピン支点の変更はないのですが,B点の連続梁の支点はピン接合点に,C点の自由端は固定端に変更することを忘れないでください.
上図のような荷重が加わったときのC点,D点のモーメントMC,MDがδC,δDとなるので,上図のような弾性荷重が加わったときの支点反力を求めましょう.
三角形荷重を等価な集中荷重に置き換えて考えましょう.
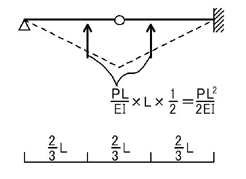
上図のような集中荷重に置き換えることができますね.次に,B点のピン接合点で,単純梁と片持ち梁の2つに分解して考えましょう.
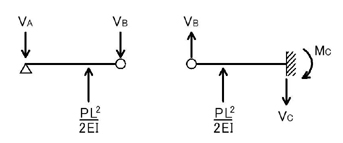
上図のように2つに分解すると,

となり,C点のたわみδCが求まります.続いて,D点のたわみδDを求めましょう.
D点のモーメントMDを求めればいいのでね.下図の三角形荷重を等価な集中荷重に置き換えてみましょう.
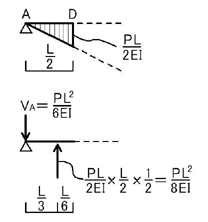
上図のようになることがわかると思います.
よってMDは
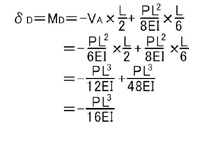
となり,δDが求まります.
ここで気づいた人もいるかもしれませんが,δCは「たわみ」の問題コード14061の問題でした.
新問対策として,少し類題を解いてみましょう.
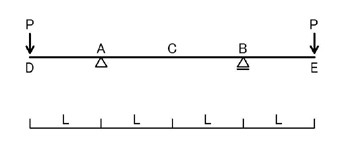
の問題を考えて見ましょう.C点とD点(E点)のたわみを求めてみましょう.
まずは支点反力を考えます.

左右対称であるため,上図のようになりますよね.
で,次にモーメント図を考えましょう.下図のようになりますね.
次に,弾性荷重を考えましょう.
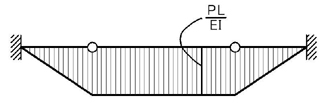
支点の変更はOKですか?
この弾性荷重が加わったときのMC,MDを求めるわけですから,まずは支点反力を求めましょう.
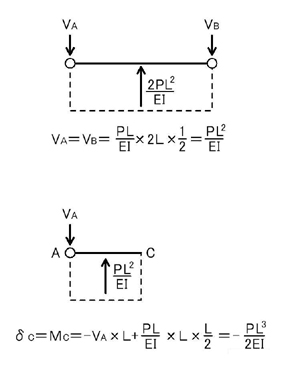
以上により,δCは求まりますね.
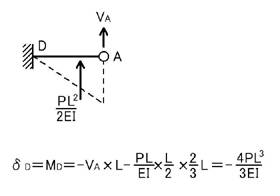
により,δD(=δE)も求まります.
クドイですが,もう一問いきましょう.
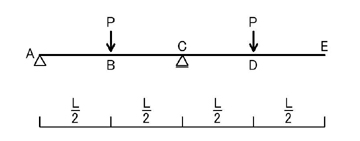
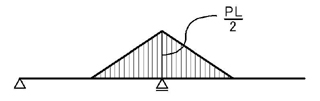
の問題において,E点のたわみδEを求めてみましょう.
以下の説明は,ポイントの抜粋にしますね.各自で解いてみてください.
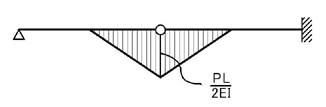
モーメント図は
となります.よって,支点の変更に注意して,弾性荷重を考えると
となります.単純梁と片持ち梁に分解すると,単純梁の支点反力は
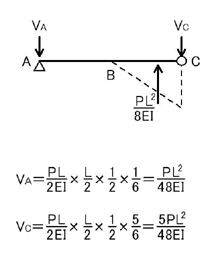
となるため,片持ち梁の先端(C点)に上向きにVCを与えてあげると
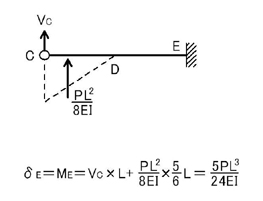
となり,δEが求まりますね.
ここで,「モールの定理」の元になっている考え方に関して説明します.たわみ曲線の微分方程式のことなんですが,「ビ,ビ,ビブン方程式~!?」っていう反応を示す人が多いと思うので,ここでは,結論のみ記載します.詳細を知りたい人は,力学の教科書を見て下さいね.
で,まず最初になぜここで「たわみ曲線の微分方程式」について書くのかについて説明します.
「たわみ」のインプットのコツにおいて,ポイント1.として「たわみ」「回転角」の基本形は覚えよう!という説明をしました.これは,微分・積分アレルギーの人が非常に多いため,最小限の暗記項目で乗り切ろう!という方向性からの説明です.しかし,簡単な微分・積分の計算をすることはOKなので,できるだけ暗記項目を減らしたいという人もいます.文章問題(計画,構造,施工)で暗記することが非常に多いため,この意見も十分理解できます.そこで,たわみと回転角については,「基本形」に関しても計算で行う方法を説明します.
勿論,微分・積分アレルギーの人は,以下の説明については見なくてもいいですよ.
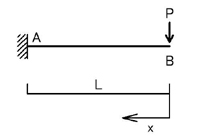
上図の片持ち梁で説明します.
B点から任意の点x(B点からの距離がxである点)でのモーメントMxは,Mx=Pxとなります.
ここで,任意の点(B点から距離xである点)の回転角θは以下の式で表すことができます(結果のみ示します).

任意の点(B点から距離xである点)のたわみδは以下の式で表すことができます(結果のみ示します).

よって,片持ち梁の先端(B点)のたわみ,回転角は(上記式において,x=0とすると)
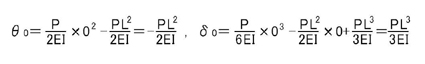
となり,片持ち梁の中央部分のたわみ,回転角は(上記式において,x=L/2とすると)
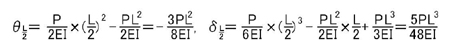
となります.
当然,「たわみ」のインプットのコツのポイント1.「たわみ」「回転角」の基本形に関しても,上記計算で求めることができます.
最後になりますが,外力が集中荷重ではなく,等分布荷重の場合にモールの定理を用いて計算することは得策ではありません.考え方としては,モールの定理で計算することができるのですが,弾性荷重を考える際に,集中荷重の場合は三角形荷重となるため等価な集中荷重に置き換えることがやりやすいのですが,等分布荷重の場合は難しいからです.
もし,等分布荷重の時は
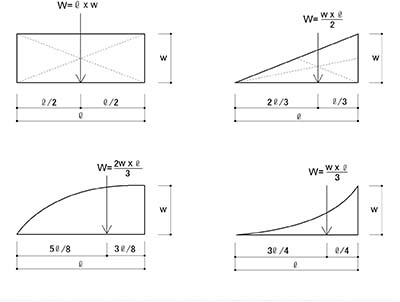
の下側(上側は集中荷重の時)を参考にしてください.
等分布荷重の場合には,上記で説明した「たわみ曲線の微分方程式」で求めることもできます.
また,建築士試験の場合は記述式の試験ではなく,4択の選択式の試験であるため,等分布荷重がかかった問題の場合には,まずモーメント図を描いて,弾性荷重を考えるときに,ほぼ同値とみなせる集中荷重に変換することで,モールの定理を用いて,等分布荷重がかかるときのたわみの近似値を求めることもできます.
しかし,これは最後の悪あがきとしての考え方の一つであると考えてください.






